


Next: Korrektheit Sequentieller Systeme
Up: FGDI3-Formelblaetter
Previous: FGDI3-Formelblaetter
- Transitionssystem
-
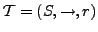
- Zustände
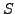
- Transitionsrelation
-
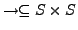
- infix notiert:
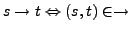
- Anfangszustand
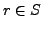 a
a
- Pfad
- der Länge
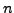 , mit
, mit
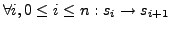
- Ausführung
- falls
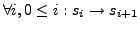
- Wörter
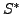 sind endlich,
sind endlich,
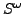 sind unendlich
sind unendlich
- Element
-
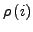 ist das
ist das 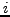 -te Element von
-te Element von
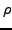 (ab 0 Zählen!)
(ab 0 Zählen!)
- Suffix
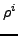 ist das bei
ist das bei 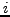 beginnende suffix von
beginnende suffix von
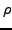 (ab 0 Zählen!)
(ab 0 Zählen!)
- Kripke Struktur
-
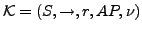
- Transitionssystem
- das zugrunde liegt
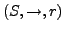
- Grundaussagen
- Menge
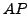
- Interpretationen
- der Grundaussagen
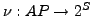
- Die Zustände haben als eine Menge von Flags
- Bild
-
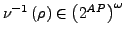 kann jeder Ausführung
kann jeder Ausführung 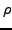 zugeordnet werden:
zugeordnet werden:
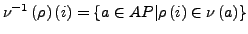
- erfüllt
-
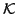 erfüllt eine LTL Formel
erfüllt eine LTL Formel 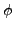 (geschrieben
(geschrieben
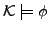 ) falls für alle bei
) falls für alle bei 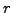 beginnenden Ausführungen
beginnenden Ausführungen
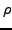 gilt, dass
gilt, dass
![$ \nu^{-1}\left(\rho\right)\subseteq\left[\left[\phi\right]\right]$](img27.png)
- Es kann sowohl
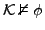 als auch
als auch
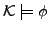 gelten!
gelten!
- LTL
- Formeln
- Ist
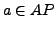 so ist
so ist 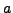 eine Formel
eine Formel
- Sind
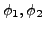 Formeln, so auch
Formeln, so auch
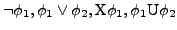
- Jede Formel definiert eine Menge von Wörtern aus
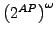 .
Sei
.
Sei
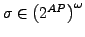
- Semantik
![$ \left[\left[\phi\right]\right]=\left\{ \sigma\vert\sigma\models\phi\right\} $](img35.png)
-
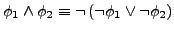
-
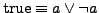
-
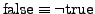
-
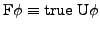
-
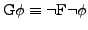
-
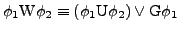
-
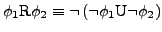
-
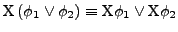
-
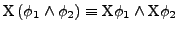
-
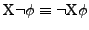
-
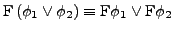
-
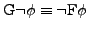
-
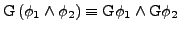
-
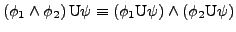
-
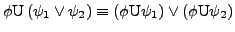
-
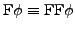
-
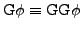
-
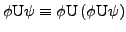
-
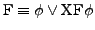
-
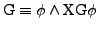
-
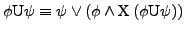
-
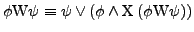
- Büchi-Automat
-
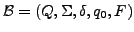
- Zustandsmenge
- (endlich)
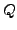
- Alphabet
- (endlich)

- Übergangsrelation
-
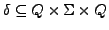
- Anfangszustand
-
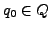
- akzeptierende
- Zustände
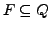
- akzeptiert
-
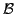 akzeptiert
akzeptiert
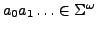 ,
gdw.
,
gdw.
-
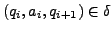 für alle
für alle 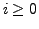
- Es gilt
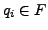 für unendlich viele
für unendlich viele 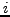
- Sprache
-
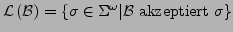
- von Büchi Automaten erkannte Sprachen heißen
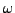 -regulär
-regulär
- Generalisierter Büchi Automat
- hat eine Menge
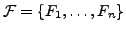 von Akzeptanzmengen. Er akzeptiert, falls unenedlich viele zustände
in
von Akzeptanzmengen. Er akzeptiert, falls unenedlich viele zustände
in 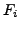 für jedes
für jedes 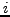 .
.
- markiertes Produckt
-
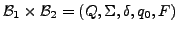
- gegeben
-
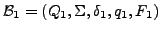 und
und
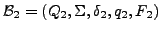
- LTL
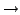 generalisierter Büchi
generalisierter Büchi
-
- gegeben
- LTL-Formel
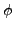 in Normalform, d.h. Negationen
sind nach Innen geschoben.
in Normalform, d.h. Negationen
sind nach Innen geschoben.
- gesucht
-
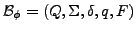
- Abschluss
-
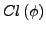 einer Formel
einer Formel 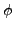 ist
die Menge aller Unterformeln von
ist
die Menge aller Unterformeln von 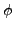 und ihrer Negierungen
und ihrer Negierungen
- Alphabet
-
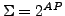 mit
mit 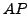 den Atomen von
den Atomen von 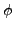
- Zustände
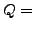 Elemente von
Elemente von
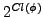 ,
die folgende Zusatzbedingungen erfüllen
,
die folgende Zusatzbedingungen erfüllen
- Anfangszustände,
- alle die
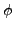 enthalten
enthalten
- Übergänge
-
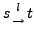 , falls
, falls
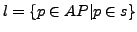 ,
sowie
,
sowie
- Akzeptierende Zustände
- Für jede Unterformel der Form
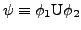 gibt es eine Akzeptanzmenge
gibt es eine Akzeptanzmenge 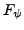 wie folgt:
wie folgt:
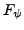 ist die Menge der Zustände, die
ist die Menge der Zustände, die 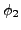 oder
oder
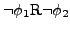 enthalten
enthalten
- Kripke
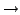 Büchi
Büchi
-
- Aktionen
-
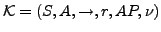
-
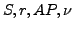 wie bei Kripkestruktur
wie bei Kripkestruktur
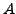 sei eine Menge von Aktionen
sei eine Menge von Aktionen
-
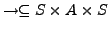
- Sei
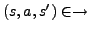 deterministisch,
so dass sich schreiben lässt
deterministisch,
so dass sich schreiben lässt
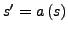
-
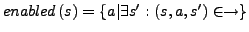
- Unabhängigkeit
-
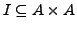 heißt Unabhängigkeitsrelation
für
heißt Unabhängigkeitsrelation
für
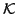 , falls
, falls
-
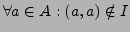
-
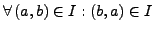
-
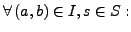 Aktiviertheit:
Aktiviertheit:
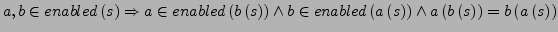
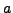 und
und 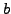 heißen unabhängig, falls
heißen unabhängig, falls
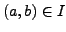
- stotter äquivalenz
- sind zwei Abläufe einer Kripke Struktur
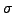 und
und 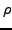 , falls es Sequenzen
, falls es Sequenzen
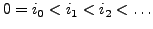 und
und
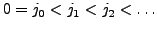 gibt, so dass für alle
gibt, so dass für alle 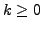 gilt:
gilt:
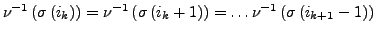
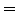
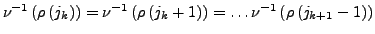
- Sichtbarkeit
- Eine Aktion
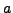 heißt unsichtbar,
falls für alle
heißt unsichtbar,
falls für alle 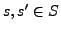 gilt: Falls
gilt: Falls
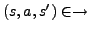 ,
dann gilt
,
dann gilt
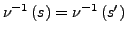 .
.
- Ample sets
-
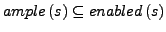 ist die Menge an Nachfolgerzuständen die tatsächlich überprüft werden
muss, beim Testen auf Leerheit der Sprache.
ist die Menge an Nachfolgerzuständen die tatsächlich überprüft werden
muss, beim Testen auf Leerheit der Sprache.
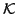 wird also
auf
wird also
auf
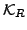 reduziert.
reduziert.
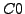 :
:
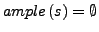
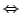
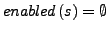
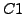 : Auf jedem Pfad beginnend in
: Auf jedem Pfad beginnend in 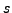 in
in
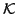 gilt: keine Aktion, die von einer Aktion in
gilt: keine Aktion, die von einer Aktion in
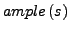 abhängt, kann vor einer Aktion in
abhängt, kann vor einer Aktion in
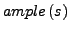 ausgeführt
werden.
ausgeführt
werden.
Eine Aktion 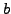 , die von einer Aktion
, die von einer Aktion
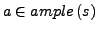 abhängt, d.h.
abhängt, d.h.
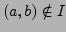 , kann erst nach der Ausführung
einer Aktion
, kann erst nach der Ausführung
einer Aktion
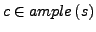 ausgeführt werden.
ausgeführt werden.
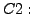 Falls
Falls
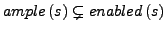 ,
sind alle Aktionen in
,
sind alle Aktionen in
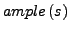 unsichtbar
unsichtbar
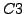 : Für alle Zyklen in
: Für alle Zyklen in
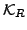 gilt: falls
gilt: falls
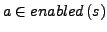 für einen Zustand im Zyklus, dann
für einen Zustand im Zyklus, dann
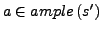 für
einen Zustand
für
einen Zustand 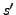 im Zyklus
im Zyklus



Next: Korrektheit Sequentieller Systeme
Up: FGDI3-Formelblaetter
Previous: FGDI3-Formelblaetter
Marco Möller 19:09:34 06.03.2006
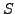
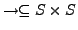
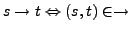
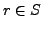 a
a
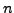 , mit
, mit
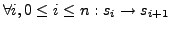
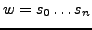
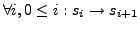
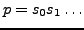
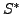 sind endlich,
sind endlich,
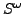 sind unendlich
sind unendlich
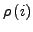 ist das
ist das 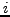 -te Element von
-te Element von
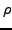 (ab 0 Zählen!)
(ab 0 Zählen!)
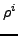 ist das bei
ist das bei 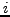 beginnende suffix von
beginnende suffix von
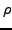 (ab 0 Zählen!)
(ab 0 Zählen!)
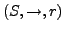
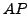
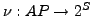
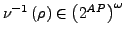 kann jeder Ausführung
kann jeder Ausführung 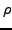 zugeordnet werden:
zugeordnet werden:
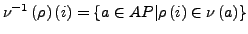
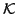 erfüllt eine LTL Formel
erfüllt eine LTL Formel 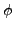 (geschrieben
(geschrieben
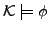 ) falls für alle bei
) falls für alle bei 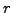 beginnenden Ausführungen
beginnenden Ausführungen
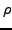 gilt, dass
gilt, dass
![$ \nu^{-1}\left(\rho\right)\subseteq\left[\left[\phi\right]\right]$](img27.png)
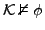 als auch
als auch
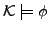 gelten!
gelten!