


Next: About this document ...
Up: FGDI3-Formelblaetter
Previous: Korrektheit Reaktiver Systeme
Alle volgenden Sysmbole müssen eindeutig zuordbar sein
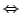 alle Mengen sind disjunkt. Bei
alle Mengen sind disjunkt. Bei 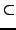 ist die gleichheit nicht
ausgeschlossen
ist die gleichheit nicht
ausgeschlossen
- Sorten
-
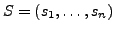 wie Liste von
Datentypen
wie Liste von
Datentypen
- Signatur
-
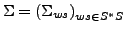 Angabe über Fuktionssymbole mit dazugehörigen Stelligkeiten und Sorten.
Angabe über Fuktionssymbole mit dazugehörigen Stelligkeiten und Sorten.
0-stellig 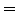 Konstante
Konstante
- Variablensymbole
-
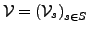
-
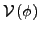 Menge aller Variablen Symbole
in
Menge aller Variablen Symbole
in 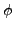
-
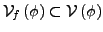 Menge aller freien Variablen Symbole in
Menge aller freien Variablen Symbole in 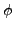 , also die nicht abquantifizierten
, also die nicht abquantifizierten
- Terme
-
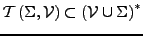 Menge der syntaktisch korrekten Terme aus den angegebenen Funktionen
und Variablen
Menge der syntaktisch korrekten Terme aus den angegebenen Funktionen
und Variablen
- Grundterme
-
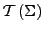 Terme ohne
Variablen
Terme ohne
Variablen
- sensible
- Signatur hat von jeder Sorte mindestens ein Konstantensymbol
 -Algebra
-Algebra- ist paar
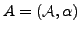 mit
mit
- Trägermengen
-
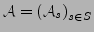
- Deutungsfunktionen
-
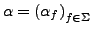 die Signatur von
die Signatur von 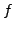 respektiert
respektiert
- Deutung
-
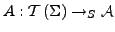 bei gegebener
bei gegebener  -Algebra
-Algebra 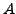
- Formeln
-
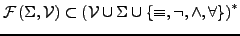
- Sprache wird auch um andere gewohnte boolsche Operatoren erweitert
-
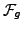 Menge der geschlossenen Formeln, enthalten
keine freien Variablen
Menge der geschlossenen Formeln, enthalten
keine freien Variablen
- Atomare Formeln
-
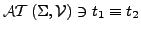 mit
mit
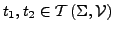
- pränexe Normalform
- ist eine Formel
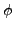 wenn alle Quantoren
wenn alle Quantoren
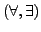 ganz links stehen.
ganz links stehen.
- universelle Formeln
- wenn pränex und alle Quantoren
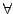
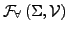 ist
Menge aller solcher Formeln über geg. Signatur
ist
Menge aller solcher Formeln über geg. Signatur
- Gleichung
- siehe Atomate Formel
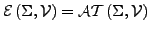
- universelle Gleichung
- universelle Formel, die hinter den
Quantoren nur nich genau ein
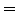 steht
steht
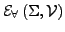 ist
die Menge aller solcher universelller Geichungen
ist
die Menge aller solcher universelller Geichungen
- Allabschluss
- für ein
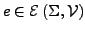 ist
ist 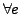 die Gleichung, in der alle freien Variablen abquantifiziert
wurden. Analog für Formelmengen.
die Gleichung, in der alle freien Variablen abquantifiziert
wurden. Analog für Formelmengen.
 -Interpretation
-Interpretation- ist ein Paar
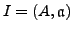 mit der
mit der  -Algebra
-Algebra 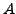 und
und
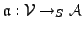 .
.
- Deutung
- von Formel:
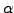 auf Funktionen und
auf Funktionen und
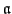 auf Variablen rekursiv anwenden. Atomare Formeln liefern bool. Dieses
mit Boolschen Funktionen verknüpfen.
auf Variablen rekursiv anwenden. Atomare Formeln liefern bool. Dieses
mit Boolschen Funktionen verknüpfen.
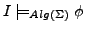
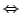 die
die  -Interpretation
-Interpretation 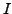 erfüllt eine Formel
erfüllt eine Formel
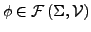 gdw. die Auswertung true liefert.
gdw. die Auswertung true liefert.
- erfüllbar
- ist
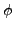 gdw. es einer
gdw. es einer  -Interpreation
-Interpreation
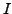 gibt die Formel
gibt die Formel 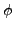 erfüllt
erfüllt
- allgemeingültig
- ist
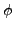 gdw. jede
gdw. jede  -Interpreation
-Interpreation
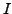 die Formel
die Formel 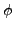 erfüllt
erfüllt
- folgt
-
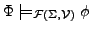
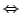 eine Formel
eine Formel 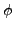 folgt aus einer Formelmenge
folgt aus einer Formelmenge
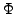 , gdw. alle Interpretationen die
, gdw. alle Interpretationen die 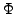 wahr machen, auch
wahr machen, auch
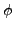 wahr machen.
wahr machen.
- Folgerungen
-
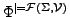 ist die Menge aller Folgerungen aus
ist die Menge aller Folgerungen aus 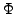
- allgemeingültig
- wenn
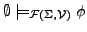
- äquivalent
-
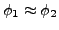 gdw.
gdw.
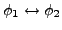 allgeimeingültig
allgeimeingültig
- Theorie
-
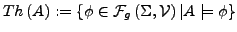 zu gegebener
zu gegebener  -Algebra
-Algebra 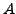
- ist angeschlossen und vollständig
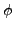 oder
oder 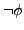 sind
(nicht)enthalten in
sind
(nicht)enthalten in
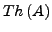
-
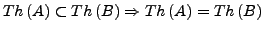
- Substitution
-
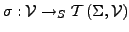
- rekursiv erweitern für gesamte Terme
- Grundsubstitution
-
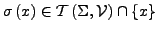 für alle
für alle
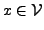
- Substitutionlemma
-
![$ \mathfrak{a}\left(\sigma\left(t\right)\right)=\mathfrak{a}\left[x_{1}/\mathfra...
...t(t_{1}\right),\ldots,x_{n}/\mathfrak{a}\left(t_{n}\right)\right]\left(t\right)$](img223.png)
-
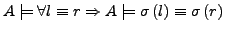 für bel. Substitution
für bel. Substitution 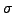
- Klasse der
 -Algebren
-Algebren
-
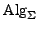
- Für
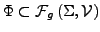 ist
ist
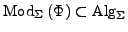 die Klasse aller
die Klasse aller  -Algebren
-Algebren 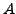 mit
mit
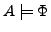
 -Homomorphismus
-Homomorphismus- Für
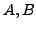
 -Algebren ist
-Algebren ist
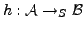 ein Homomorphismus wenn
ein Homomorphismus wenn
-
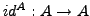 ist Homomorphismus
ist Homomorphismus
- Verkettung von Homomorphismen ist wieder Homomorphismus
-
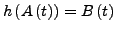 für alle
für alle
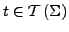
- Äquivalenzrelation
- ist
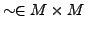 wenn
wenn
- reflexiv
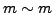
- symmetrisch
-
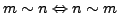
- transitiv
-
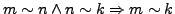
- Für Mengen
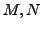 und
und
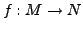 ist
ist 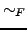 definiert durch
definiert durch
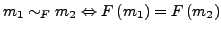 eine Äquivalenzrelation
eine Äquivalenzrelation
- Äquivalenzklassen sind disjunkte Zerlegung der Gesamtmenge
- Äquivalenzklasse
-
![$ \left[m\right]_{\sim}=\left\{ n\in M\vert n\sim m\right\} \subset2^{M}$](img243.png)
- Quotientenmenge
-
![$ M/_{\sim}=\left\{ \left[m\right]_{\sim}\in2^{M}\vert m\in M\right\} $](img244.png)
 -Isomorphismus
-Isomorphismus- ist eine bijektiver Homomorphismus
-
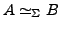 sind zwei
sind zwei  -Algebren, wenn ein
isomorphismus zwischen ihnen exisitert
-Algebren, wenn ein
isomorphismus zwischen ihnen exisitert
-
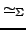 ist Äquivalenzrelation
ist Äquivalenzrelation
- Isomorphe Algebren haben gleiche Theorie
- Abstrakter Datentyp
- für eine Signatur
 ist eine
Klasse
ist eine
Klasse
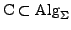 von
von  -Algebren,
die unter Isomorphie abgeschlossen ist, d.h. es gilt für alle
-Algebren,
die unter Isomorphie abgeschlossen ist, d.h. es gilt für alle
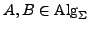
- initial
- ist eine
 -Algebra
-Algebra
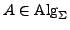 gdw. gilt: Für jede
gdw. gilt: Für jede  -Algebra
-Algebra 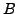 existiert genau
ein
existiert genau
ein  -Homomorphismus von
-Homomorphismus von 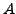 nach
nach 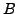 .
.
- gilt
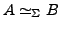 ist auch
ist auch 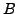 initial
initial
- Termalgebren
- Sei
 eine Signatur bzgl. einer Sortenmenge
eine Signatur bzgl. einer Sortenmenge
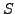 . Dann ist die Termalgebra
. Dann ist die Termalgebra
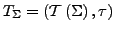 definiert durch
definiert durch
- Diese Termalgebra ist inital in der Klasse aller
 -Algebren
-Algebren
- Kongruenzrelation
- ist
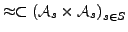 wenn:
wenn:
- Quotientenalgebra
- ist eine
 -Algebra zu gegebenen
-Algebra zu gegebenen
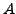 und
und 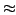 :
:
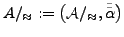 mit
mit
- Quotiententermalgebra
- Für eine
 -Algebra
-Algebra 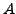 sei
sei
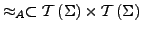 für alle
für alle
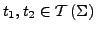 definiert
durch
die Quotiententermalgebra von
definiert
durch
die Quotiententermalgebra von 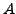 ist dann definiert als
ist dann definiert als
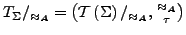
- Für Variablenbelegung
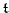 und Term
und Term 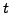 gilt
gilt
![$ \mathfrak{t}\left(t\right)=\left[t\right]_{\approx_{A}}$](img270.png)
- kanonische Termalgebra
- heißt
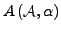 gdw.:
gdw.:
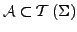 und
und
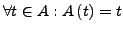
- Teilsignatur
- ist eine Signatur, bei der einige Funktionssymbole
weggleassen wurden
- Erzeugte
 -Algebra
-Algebra
- Seien
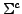 und
und 
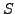 -Signaturen mit
-Signaturen mit
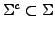 und sei
und sei
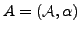 eine
eine  -Algebra. Dann ist
-Algebra. Dann ist 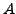 durch
durch
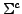 erzeugt
gdw. gilt:
erzeugt
gdw. gilt:
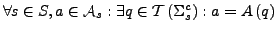
- bei erzeugter Algebra sind alle Trägermengen abzählbar
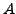 initial
initial
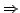
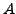 erzeugt
erzeugt
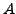 erzeugt
erzeugt
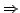
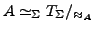
- Sei
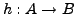 Homomorphismus ist eindeutig, falls
Homomorphismus ist eindeutig, falls
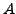 erzeugt
erzeugt
- erzeugte Algebren mit gleicher Theorie sind isomorph
- frei
- erzeugt wenn zusätzlich gilt
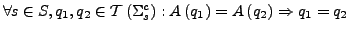
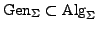 bezeichnet
die Klasse aller erzeugten
bezeichnet
die Klasse aller erzeugten  -Algebren
-Algebren
- (frei) erzeugtheit vererbt sich durch Isomorphie und Quotiententermalgebra
bildung
- alle Konstruktoren werden als injektive Funktionen gedeutet
- Es existiert eine isomorphe kanonische Termalgebra
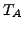 zu
zu 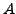
- Redukt
- ist Reduzierte Algebra zu kleinerer Signatur
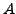 durch
durch
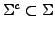 erzeugt und sei
erzeugt und sei 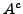 das
das
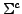 Redukt von
Redukt von 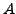
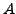 freu erzeugt durch
freu erzeugt durch
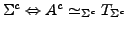
- Expansion
- ist vollständige Algebra zu großer Signatur
- Kongruenz aus Relation
- Sei
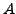 eine
eine  -Algebra,
und
-Algebra,
und
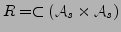 .
Es existiert eine kleinste Kongruenzrelation
.
Es existiert eine kleinste Kongruenzrelation
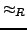 die
die 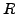 noch enthält
noch enthält
- Kongruenz aus Gleichung
- Für
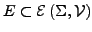 ist
ist
und
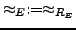
- Für alle
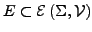 gilt
gilt
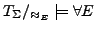
- Sei
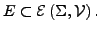 Dann
ist
Dann
ist
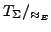 initial in
initial in
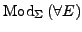
- Vorgehen
- Gegeben sei
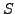 ,
,
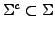 und
und
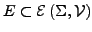 , so dass
, so dass
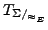 eine durch
eine durch
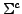 freu erzeugte Quotiententermalgebra ist.
freu erzeugte Quotiententermalgebra ist.
- structure
- struct <=
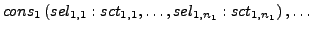
-
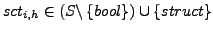 für alle
für alle
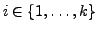 und alle
und alle
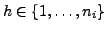 .
(
.
(
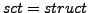 )
)
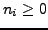 für alle
für alle
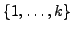
- Anzahl der Konstruktoren:
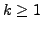
- Axiome
-
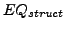
- Gleichheit von Konstanten
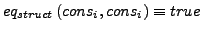
- Gleichheit von längeren Konstruktoren (geschachtelt, allquantifiziert)
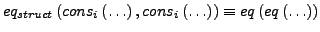
- Nichgleichheit bei führenden Konstruktoren
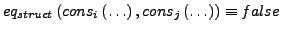
- Falsch angewendete Selektoren liefern Beispielterm (Konstante)
- Selektoren
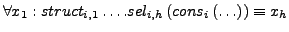
-
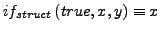
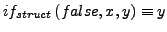
- function
-
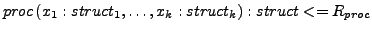
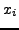 Parameter vom Typ
Parameter vom Typ

- name
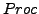 und Rückgabe vom Typ
und Rückgabe vom Typ 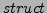
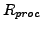 ist Rumpf und muss sich zu
ist Rumpf und muss sich zu 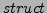 auswerten
lassen
auswerten
lassen
- konstruktive Spec.
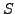 ist eine Folge
ist eine Folge
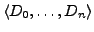 von Datenstruktur- und Prozedurdefinitionen.
von Datenstruktur- und Prozedurdefinitionen.
-
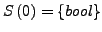 ,
,
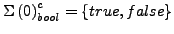 ,
,
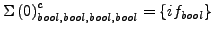
-
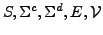 sind Funktionen von
sind Funktionen von
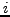
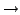 nummer der konstruktionsiteration
nummer der konstruktionsiteration
-
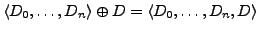
- zulässige Spec.
- Eine Konstruktive Spezifikation
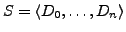 ist zulässig, gdw. die
ist zulässig, gdw. die
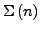 -Algebra
-Algebra
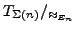 frei erzeugt durch
frei erzeugt durch
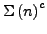 ist
ist
- Datenstrukturdefinitionen sind automatisch zulässig in Verifun
- prozedur Relation
- für gegebenes
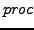 ist
ist
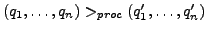 gdw. beim Aufruf von
gdw. beim Aufruf von
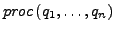 wird
wird
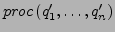 rekursiv aufgerufen
rekursiv aufgerufen
- Eine Prozedur terminiert und damit ist ihre Definition zulässig,
gdw.
 fundiert ist.
fundiert ist.
- Fundierte Relation
- Eine Relation
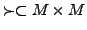 heißt fundiert gdw. es gibt keine unendliche Folgen
heißt fundiert gdw. es gibt keine unendliche Folgen
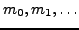 mit
mit
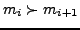 für alle
für alle



Next: About this document ...
Up: FGDI3-Formelblaetter
Previous: Korrektheit Reaktiver Systeme
Marco Möller 19:09:34 06.03.2006
![]() alle Mengen sind disjunkt. Bei
alle Mengen sind disjunkt. Bei ![]() ist die gleichheit nicht
ausgeschlossen
ist die gleichheit nicht
ausgeschlossen