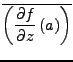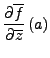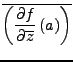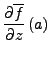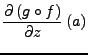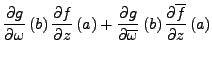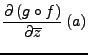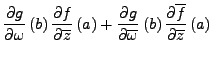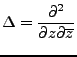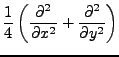Next: Cauchys Integralsatz
Up: Holomorphe Funktionen
Previous: Ableitung einer Funktionenfolge
Contents
Index
Wirtinger Kalkül
Man definiert für reell differenzierbare komplexe Funktionen die sogenannten
Wirtinger Ableitungen durch
Seien nun
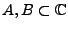 offen und
offen und
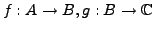 reell differenzierbar. Sei weiter
reell differenzierbar. Sei weiter 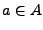 und
und
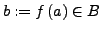 .
Definiere
.
Definiere
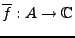 durch
durch
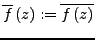 .
.
Es gilt
wobei 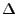 der Laplace-Operator
ist.
der Laplace-Operator
ist.





Next: Cauchys Integralsatz
Up: Holomorphe Funktionen
Previous: Ableitung einer Funktionenfolge
Contents
Index
Marco Möller 20:58:46 15.11.2006
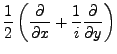
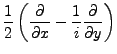
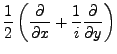
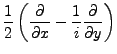
![]() offen und
offen und
![]() reell differenzierbar. Sei weiter
reell differenzierbar. Sei weiter ![]() und
und
![]() .
Definiere
.
Definiere
![]() durch
durch
![]() .
.