Sei
![]() stetig. Wir nennen
stetig. Wir nennen
![]() stückweise
stetig differenzierbar (ssd). Wenn es Zahlen
stückweise
stetig differenzierbar (ssd). Wenn es Zahlen
![]() gibt, sodass
gibt, sodass
![]() stetig
differenzierbar ist,
stetig
differenzierbar ist,
![]() .
.
Für
![]() stetig und
stetig und
![]() stückweise stetig differenzierbarer Weg (oder Kurve). Setze
stückweise stetig differenzierbarer Weg (oder Kurve). Setze
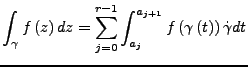
Das Ergebniss des Integrals ist also eine komplexe Zahl.
Das Integrieren ist eine lineare Abbildung. Es gilt: