




Next: Cauchys Integralsatz
Up: Cauchys Integralsatz
Previous: Sternförmige Mengen
Contents
Index
Zwei Wege
![$ \gamma_{0}:\left[0,1\right]\rightarrow X$](img170.png) und
und
![$ \gamma_{1}\left[0,1\right]\rightarrow X$](img171.png) heißen homotop, wenn es eine stetige Abbildung
heißen homotop, wenn es eine stetige Abbildung
![$ H:\left[0,1\right]\times\left[0,1\right]\rightarrow X$](img172.png) gibt mit
gibt mit
-
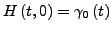
-
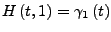
-
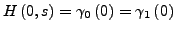
-
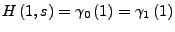
Schreibe dann
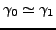 .
.
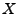 heißt einfach zusammenhängend,
wenn
heißt einfach zusammenhängend,
wenn 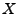 wegzusammenhängend ist und für alle Wege
wegzusammenhängend ist und für alle Wege
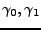 gilt: aus
gilt: aus
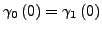 und
und
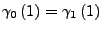 folgt stets
folgt stets
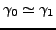 .
.
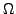 sternförmig
sternförmig
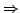
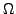 einfach zusammenhängend
einfach zusammenhängend
- einfach zusammenhängend kann man sich vorstellen, das es möglich ist
ein quadrat stetig auf
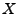 abzubilden, also enthält z.B.
abzubilden, also enthält z.B. 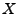 im
2dimensionalen keine ``Löcher''
im
2dimensionalen keine ``Löcher''
- Das Integral über zwei Wegen die homotopieäquivalent sind ist gleich,
wenn
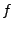 auf diesem Gebiet holomorph
auf diesem Gebiet holomorph
- Fall ein geschlossener Weg homotop zum ``Nullweg'' ist, nennt
sich dieser Null-homotop.
D.h. 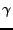 heißt null-homotop in
heißt null-homotop in 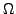 falls
falls 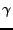 s.s.d.
geschlossen und falls es ein stetiges
s.s.d.
geschlossen und falls es ein stetiges
![$ H:\left[0,1\right]\times\left[a,b\right]\rightarrow\Omega$](img181.png) gibt mit
gibt mit
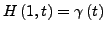 und
und
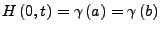 für alle
für alle 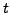 .
.
Marco Möller 20:58:46 15.11.2006
![]() und
und
![]() heißen homotop, wenn es eine stetige Abbildung
heißen homotop, wenn es eine stetige Abbildung
![]() gibt mit
gibt mit
![]() heißt einfach zusammenhängend,
wenn
heißt einfach zusammenhängend,
wenn ![]() wegzusammenhängend ist und für alle Wege
wegzusammenhängend ist und für alle Wege
![]() gilt: aus
gilt: aus
![]() und
und
![]() folgt stets
folgt stets
![]() .
.