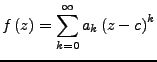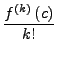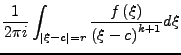Next: Äquivalente Aussagen über Holomorphe
Up: Cauchys Integralsatz
Previous: Entwicklungslemma
Contents
Index
Cauchy-Taylor Entwicklungssatz
Sei 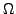 ein Gebiet,
ein Gebiet,
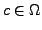 , sei
, sei 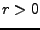 so, dass
so, dass
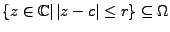 .
Sei
.
Sei
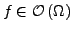 . Dann gilt
. Dann gilt
für alle
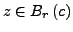 und
und
Insbesondere ist jedes
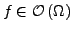 beliebig
oft
beliebig
oft
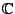 -differenzierbar.
-differenzierbar.
- Sei
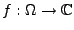 eine holomorphe Funktion auf
einem Gebiet
eine holomorphe Funktion auf
einem Gebiet
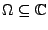 . Ferner sei
. Ferner sei
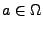 und
und
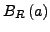 die größte offene Kreisscheibe um
die größte offene Kreisscheibe um 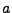 ,
die noch ganz in
,
die noch ganz in 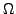 enthalten ist. Ist
enthalten ist. Ist 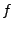 auf
auf
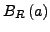 unbeschränkt, dann ist
unbeschränkt, dann ist 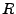 gleich den Konvergenzradius der Taylorreihe
von
gleich den Konvergenzradius der Taylorreihe
von 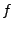 um den Entwicklungspunkt
um den Entwicklungspunkt 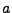 .
.
- Taylorreihe ist Spezialfall der Laurent-Reihe (siehe sub:Entwicklungssatz-von-Laurent)
mit
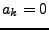 für
für 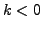 .
.
Marco Möller 20:58:46 15.11.2006
![]() ein Gebiet,
ein Gebiet,
![]() , sei
, sei ![]() so, dass
so, dass
![]() .
Sei
.
Sei
![]() . Dann gilt
. Dann gilt