




Next: Singularität
Up: Isolierte Singularitäten
Previous: Entwicklungssatz von Laurent
Contents
Index
Partialbruchzerlegung
- Polynomdivision, und die Funktion in der Form
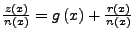 schreiben.
schreiben.
- grad von
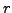 ist kleiner als grad von
ist kleiner als grad von 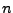
- Den Rest
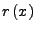 durch Partialbruchzerlegung vereinfachen,
dazu
durch Partialbruchzerlegung vereinfachen,
dazu
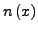 in Linearfaktoren zerlegen. Dazu die Nullstellen
in Linearfaktoren zerlegen. Dazu die Nullstellen
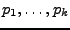 mit den Vielfachheiten
mit den Vielfachheiten
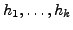
- Nun die Gleichung Ansatz für Partialbruchzerlegung aufstellen
- Falls ein Nullstelle des Nennerpolynoms
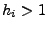 mal vorkommt, muss
man sie mehrfach als Nenner verwenden, in den Potenzen
mal vorkommt, muss
man sie mehrfach als Nenner verwenden, in den Potenzen 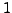 bis
bis 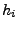 .
.
- Hauptnenner des Partialbruchs bilden und auf einen Nenner (dies ist
dann ja genau
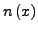 ) bringen.
) bringen.
- Für
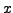 der Reihe nach
der Reihe nach 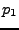 bis
bis 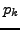 einsetzen. So erhält
man
einsetzen. So erhält
man 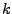 Bestimmungsgleichunen für die
Bestimmungsgleichunen für die 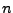 Unbekannten
Unbekannten 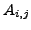
- Fertig!!
- Mit Partialbruchzerlegung lassen sich alle Gleichungen zur Summe über
geometrischen Reihen oder ähnlichem Umformen
Marco Möller 20:58:46 15.11.2006
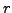 ist kleiner als grad von
ist kleiner als grad von 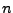
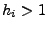 mal vorkommt, muss
man sie mehrfach als Nenner verwenden, in den Potenzen
mal vorkommt, muss
man sie mehrfach als Nenner verwenden, in den Potenzen 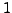 bis
bis 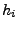 .
.