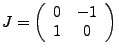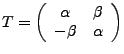Next: Cauchy-Riemann-Differentialgleichungen
Up: Holomorphe Funktionen
Previous: Eigenschaften von holomorphen Funktionen
Contents
Index
Sei
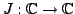 definiert durch
definiert durch
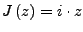 ,
dass ist eine lineare Abbildung auf
,
dass ist eine lineare Abbildung auf
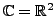 mit
mit
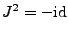 , also
, also
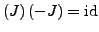 .
.
Eine lineare Abbildung
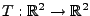 ist genau dann linear über
ist genau dann linear über
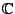 , wenn gilt
, wenn gilt
In Matritzenschreibweise mit
muss 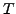 die Form haben
für beliebige
die Form haben
für beliebige
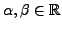 . Solche
. Solche 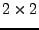 -Matrizen
werden Drehstreckungen genannt.
-Matrizen
werden Drehstreckungen genannt.
- Falls man
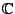 als
als
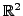 auffasst entspräche
die Multiplikation mit einer komplexen Zahl genau einer solchen Drehstreckung.
auffasst entspräche
die Multiplikation mit einer komplexen Zahl genau einer solchen Drehstreckung.
Marco Möller 20:58:46 15.11.2006
![]() definiert durch
definiert durch
![]() ,
dass ist eine lineare Abbildung auf
,
dass ist eine lineare Abbildung auf
![]() mit
mit
![]() , also
, also
![]() .
.
![]() ist genau dann linear über
ist genau dann linear über
![]() , wenn gilt
, wenn gilt