




Next: Differentialgleichung mit getrennten Variablen
Up: Vektorfelder und Flüsse
Previous: Eigenschaften von Lösungen
Contents
Index
Subsections
Zeitabhängige Vektorfelder
Gegeben 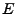 Banachraum,
Banachraum,
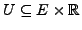 offen
offen
Gesucht ist Integralkurve
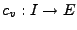 mit
mit
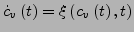 und
und
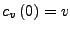 .
.
Sei
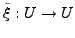 ,
,
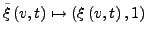 und
und
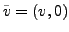 mit der Integralkurve
mit der Integralkurve
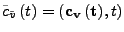 .
.
- Löse also Ersatzkurve
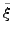 und nehme erste Komponente
und nehme erste Komponente
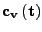 als Lösung für ursprüngliches Problem
als Lösung für ursprüngliches Problem
Parameterabhängiges Vektorfeld
Sei 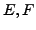 Banachräume,
Banachräume,
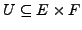 offen. Eine Abbildung
offen. Eine Abbildung
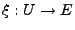 ,
,
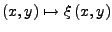 heißt parameterabhängiges Vektorfeld. Gesucht ist Integralkurve
heißt parameterabhängiges Vektorfeld. Gesucht ist Integralkurve
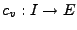 mit
mit
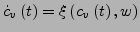 und
und
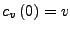 .
.
Sei
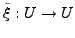 ,
,
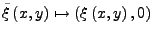 und
und
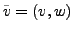 mit der Integralkurve
mit der Integralkurve
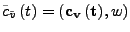 .
.
- Löse also Ersatzkurve
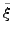 und nehme erste Komponente
und nehme erste Komponente
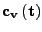 als Lösung für ursprüngliches Problem
als Lösung für ursprüngliches Problem
Vektorfelder höherer Ordnung
Sei 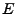 Banachraum,
Banachraum,
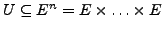 offen.
Sei
offen.
Sei
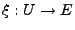 mit der gesuchten Integralkurve
mit der gesuchten Integralkurve
Betrachte das Vektorfeld
Dies hat die Integralkurve
- Löse also Ersatzkurve
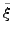 und nehme erste Komponente
und nehme erste Komponente
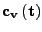 als Lösung für ursprüngliches Problem
als Lösung für ursprüngliches Problem
- Ist
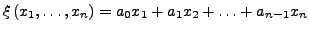 ,
,
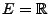 . Es gilt
. Es gilt
Anderer Startpunkt
Ist 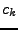 eine Integralkurve zu
eine Integralkurve zu 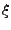 mit
mit
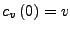 ,
so ist
,
so ist
eine Integralkurve mit
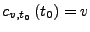 .
.
- Also erst Lösen mit Startzeitpunkt 0 und dann
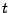 mit
mit 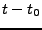 Substituieren
Substituieren





Next: Differentialgleichung mit getrennten Variablen
Up: Vektorfelder und Flüsse
Previous: Eigenschaften von Lösungen
Contents
Index
Marco Möller 12:27:24 18.02.2006
![]() Banachraum,
Banachraum,
![]() offen
offen
![]() mit
mit
![]() und
und
![]() .
.
![]() ,
,
![]() und
und
![]() mit der Integralkurve
mit der Integralkurve
![]() .
.
![]() Banachräume,
Banachräume,
![]() offen. Eine Abbildung
offen. Eine Abbildung
![]() ,
,
![]() heißt parameterabhängiges Vektorfeld. Gesucht ist Integralkurve
heißt parameterabhängiges Vektorfeld. Gesucht ist Integralkurve
![]() mit
mit
![]() und
und
![]() .
.
![]() ,
,
![]() und
und
![]() mit der Integralkurve
mit der Integralkurve
![]() .
.
![]() Banachraum,
Banachraum,
![]() offen.
Sei
offen.
Sei
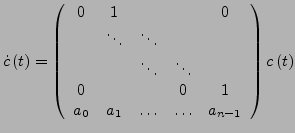
![]() mit der gesuchten Integralkurve
mit der gesuchten Integralkurve
![]() eine Integralkurve zu
eine Integralkurve zu ![]() mit
mit
![]() ,
so ist
,
so ist