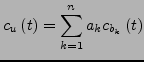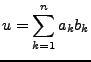Next: Lösungsraum der inhomogenen linearen
Up: Lineare Differentialgleichungen
Previous: Inhomogene DGL
Contents
Index
Sei
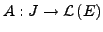 stetig,
stetig, 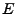 Banachraum.
Angenommen
Banachraum.
Angenommen
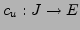 und
und
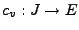 sind
Lösungen der DGL
sind
Lösungen der DGL
mit
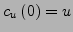 und
und
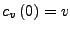 .
.
Sind
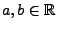 , so ist
, so ist
wieder Lösung zum Anfangswert
Die Abbildung
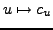 ,
,
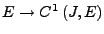 ist linear und injektiv. Das Bild dieser Abbildung
ist linear und injektiv. Das Bild dieser Abbildung
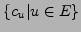 heißt Lösungsraum der lin. homogenen DGL.
Insbesondere: ist
heißt Lösungsraum der lin. homogenen DGL.
Insbesondere: ist
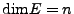 , so ist der Lösungsraum
, so ist der Lösungsraum 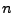 -dimensional.
Ist
-dimensional.
Ist
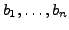 Basis von
Basis von 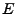 so ist
die (eindeutige) Lösung zum Anfangswert
Man nennt
so ist
die (eindeutige) Lösung zum Anfangswert
Man nennt
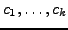 dann auch Lösungsfundamentalsystem
der homogenen lin. DGL
dann auch Lösungsfundamentalsystem
der homogenen lin. DGL
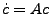 .
.
- Der Real- und Imaginärteil einer Komplexen Lösung sind wieder relle
Lösungen
- Die Spalten von
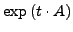 bilden ein Fundamentalsysten,
unabhängig von der konkreten Basis von A
bilden ein Fundamentalsysten,
unabhängig von der konkreten Basis von A
Marco Möller 12:27:24 18.02.2006
![]() stetig,
stetig, ![]() Banachraum.
Angenommen
Banachraum.
Angenommen
![]() und
und
![]() sind
Lösungen der DGL
sind
Lösungen der DGL
![]() , so ist
, so ist