




Next: Nachfolgerstruktur (Konstruktion von )
Up: Mengen, natürliche Zahlen, Induktion
Previous: Mengen, natürliche Zahlen, Induktion
Contents
Index
Subsections
In der Sprache der Mengenlehre gibt es nur ein fundamentales Zeichen:
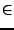
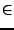 ``ist Element von''
``ist Element von''
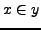 ``
``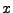 ist Element von
ist Element von 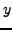 ''
''
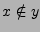 ``
``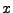 ist nicht Element von
ist nicht Element von 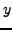 ''
''
Vereinbarung: schreibe
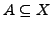 (
(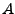 ist Teilmenge von
ist Teilmenge von  )
falls für jedes
)
falls für jedes 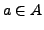 gilt
gilt 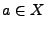 .
.
Mengen werden nach bestimmten Spielregeln gebaut, den Zermelo-Fraenkel-Axiomen
(ZFC (c wie choice)):
-
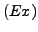 Es gibt Mengen
Es gibt Mengen
-
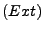 Zwei Mengen sind gleich, falls sie die gleichen
Elemente haben:
Zwei Mengen sind gleich, falls sie die gleichen
Elemente haben:
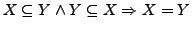
-
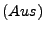 Ist
Ist  eine Menge,
eine Menge, 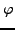 eine Formel (Bedingung),
so ist
eine Formel (Bedingung),
so ist
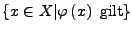 ebenfalls eine Menge (eine Teilmenge von
ebenfalls eine Menge (eine Teilmenge von  ).
).
- Die leere Menge ist definiert durch
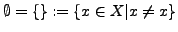
- Der Durchschnitt (Schnittmenge)
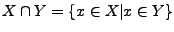
- Disjunkt heißen zwei Mengen, wenn
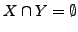
- Das Komplement
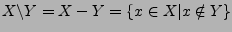
- Die symmetrische Differenz
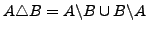
-
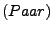 Sind
Sind 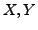 Mengen, dann gibt es eine Menge
Mengen, dann gibt es eine Menge 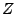 ,
deren Elemente genau
,
deren Elemente genau  und
und 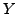 sind. (entsprechend mit mehr als
2 Mengen)
sind. (entsprechend mit mehr als
2 Mengen)
-
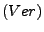 Ist
Ist  eine Menge, so gibt es eine Menge
eine Menge, so gibt es eine Menge 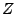 ,
deren Elemente genau die Elemente der Elemente von
,
deren Elemente genau die Elemente der Elemente von  sind,
sind,
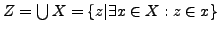
- Die Vereinigung von zwei Mengen lässt sich
auch so schreiben:
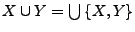
- Für die Vereinigung von disjunkten Mengen
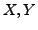 schreibe auch
schreibe auch
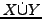
-
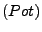 Ist X eine Menge, so gibt es eine Menge, deren
Elemente genau die Teilmengen von
Ist X eine Menge, so gibt es eine Menge, deren
Elemente genau die Teilmengen von  sind, die Potenzmenge
sind, die Potenzmenge
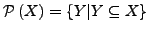 .
.
-
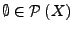
-
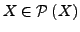
-
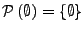
- Ist
 endlich mit
endlich mit 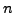 Elementen, so hat die Potenzmenge
Elementen, so hat die Potenzmenge 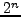 Elemente
Elemente
- Ist
 endlich mit
endlich mit 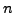 Elementen, so gibt es genau
Elementen, so gibt es genau
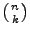
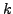 -elementige Mengen in der Potenzmenge von
-elementige Mengen in der Potenzmenge von  (bzw.
(bzw. 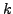 -elementige
Teilmengen in
-elementige
Teilmengen in  )
)
-
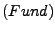 Es gibt keine bodenlosen
Mengen. Ist
Es gibt keine bodenlosen
Mengen. Ist  eine nichtleere Menge, so gibt es ein
eine nichtleere Menge, so gibt es ein 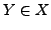 mit
mit
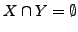
- für keine Menge
 kann gelten
kann gelten 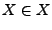
- Die ``Russelmenge''
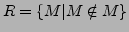 ist nach den Axiomen keine Menge.
ist nach den Axiomen keine Menge.
-
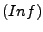 Es gibt unendliche Mengen.
Es gibt unendliche Mengen.
-
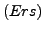 Ist
Ist
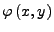 eine Formel, die
einer Menge
eine Formel, die
einer Menge 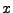 eine neue Menge
eine neue Menge 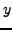 zuordnet, und ist
zuordnet, und ist  eine
Menge, so ist auch
eine
Menge, so ist auch
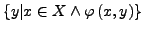 eine Menge.
eine Menge.
-
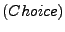 Ist
Ist  eine nichtleere Menge mit der Eigenschaft,
dass alle Elemente von
eine nichtleere Menge mit der Eigenschaft,
dass alle Elemente von  disjunkt sind, so gibt es eine Menge
disjunkt sind, so gibt es eine Menge 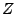 ,
die mit jedem Element von
,
die mit jedem Element von  genau ein Element gemeinsam hat. (Teilweise
umstrittenes Axiom)
genau ein Element gemeinsam hat. (Teilweise
umstrittenes Axiom)
- Komplementbildung
Sei
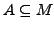 dann ist
dann ist
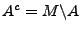
- Distributivgesetz
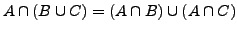
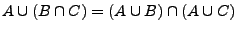
- de Morgan'sch Regel
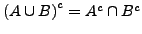
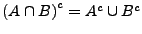
Ein geordnetes Paar
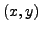 hat eine erste Komponente
hat eine erste Komponente 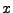 und eine zweite Komponente
und eine zweite Komponente 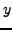 . In
der Sprache der Mengenlehre setzt man
. In
der Sprache der Mengenlehre setzt man
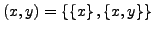 .
Es gilt
.
Es gilt
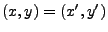 genau dann, wenn
genau dann, wenn 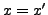 und
und 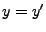 .
.
Das kartesische Produkt 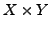 zweier Mengen
zweier Mengen 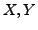 ist
ist
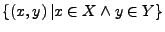 .
Ist
.
Ist 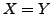 schreibt man
schreibt man
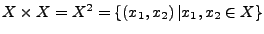 .
Dieses lässt sich Iterrieren zu Produkten
.
Dieses lässt sich Iterrieren zu Produkten
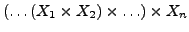 .
Die Klammern sind nicht wichtig, wir lassen sie weg. Ist
.
Die Klammern sind nicht wichtig, wir lassen sie weg. Ist
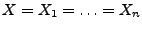 ,
schreiben wir
,
schreiben wir
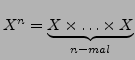 .
Die Elemente dieser Menge heißen
.
Die Elemente dieser Menge heißen 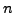 -Tupel.
-Tupel.
Sei
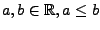 .
.
Die Menge
![$ \left[a,b\right]=\left\{ x\in\mathbb{R}\vert a\le x\le b\right\} $](img198.png) heißt abgeschlossenes endliches Intervall
(abgeschlossenes beschränktes Inervall).
heißt abgeschlossenes endliches Intervall
(abgeschlossenes beschränktes Inervall).
Die Menge
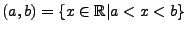 heißt offenes endliches Intervall.
heißt offenes endliches Intervall.
- andere Schreibweise auch gebäuchlich:
![$ \left(a,b\right)=\left]a,b\right[$](img200.png)
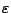 -Umgebung
-Umgebung
Für
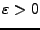 heißt die Menge
heißt die Menge
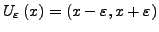
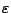 -Umgebung von
-Umgebung von 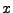 .
.
offene Menge
Eine Menge  heißt offen, falls es zu jedem
Punkt
heißt offen, falls es zu jedem
Punkt 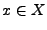 eine
eine
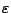 -Umgebung
-Umgebung
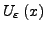 gibt, welche ganz in
gibt, welche ganz in  liegt. Mit Qantoren:
liegt. Mit Qantoren:
-
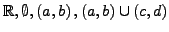 sind offene Mengen
sind offene Mengen
-
![$ \mathbb{N},\mathbb{Z},\mathbb{Q},\left[a,b\right]$](img207.png) sind nicht
offen
sind nicht
offen





Next: Nachfolgerstruktur (Konstruktion von )
Up: Mengen, natürliche Zahlen, Induktion
Previous: Mengen, natürliche Zahlen, Induktion
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]()
![]() hat eine erste Komponente
hat eine erste Komponente ![]() und eine zweite Komponente
und eine zweite Komponente ![]() . In
der Sprache der Mengenlehre setzt man
. In
der Sprache der Mengenlehre setzt man
![]() .
Es gilt
.
Es gilt
![]() genau dann, wenn
genau dann, wenn ![]() und
und ![]() .
.
![]() zweier Mengen
zweier Mengen ![]() ist
ist
![]() .
Ist
.
Ist ![]() schreibt man
schreibt man
![]() .
Dieses lässt sich Iterrieren zu Produkten
.
Dieses lässt sich Iterrieren zu Produkten
![]() .
Die Klammern sind nicht wichtig, wir lassen sie weg. Ist
.
Die Klammern sind nicht wichtig, wir lassen sie weg. Ist
![]() ,
schreiben wir
,
schreiben wir
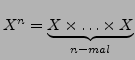 .
Die Elemente dieser Menge heißen
.
Die Elemente dieser Menge heißen ![]() -Tupel.
-Tupel.
![]() .
.
![]() heißt abgeschlossenes endliches Intervall
(abgeschlossenes beschränktes Inervall).
heißt abgeschlossenes endliches Intervall
(abgeschlossenes beschränktes Inervall).
![]() heißt offenes endliches Intervall.
heißt offenes endliches Intervall.
![]() heißt die Menge
heißt die Menge
![]()
![]() -Umgebung von
-Umgebung von ![]() .
.
![]() heißt offen, falls es zu jedem
Punkt
heißt offen, falls es zu jedem
Punkt ![]() eine
eine
![]() -Umgebung
-Umgebung
![]() gibt, welche ganz in
gibt, welche ganz in ![]() liegt. Mit Qantoren:
liegt. Mit Qantoren: