




Next: Relationen
Up: Mengen, natürliche Zahlen, Induktion
Previous: Mengen
Contents
Index
Subsections
Nachfolgerstruktur (Konstruktion von
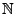 )
)
Eine Menge 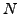 mit einer Abbildung
mit einer Abbildung
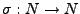 (
(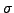 heiße Nachfolgerabbildung) heißt Nachfolgerstruktur,
falls sie die Peano-Axiome erfüllt:
heiße Nachfolgerabbildung) heißt Nachfolgerstruktur,
falls sie die Peano-Axiome erfüllt:
-
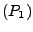 Es gibt ein Element
Es gibt ein Element 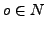 , so dass
, so dass
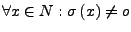
-
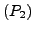 Aus
Aus
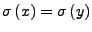 folgt
folgt 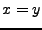 (
(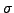 ist injektiv)
ist injektiv)
-
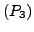 Ist
Ist
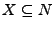 eine Teilmenge, und gilt
eine Teilmenge, und gilt
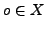 , und folgt aus
, und folgt aus
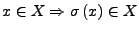 (d.h.
(d.h.  ist abgeschlossen unter der Nachfolgerfunktion) so gilt
ist abgeschlossen unter der Nachfolgerfunktion) so gilt
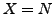 .
.
-
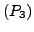 ist das Axiom der vollständigen Induktion.
ist das Axiom der vollständigen Induktion.
- Es gibt genau eine Nachfolgerstruktur mit
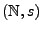 mit
mit
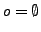 und
und
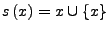
- Ist
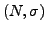 eine Nachfolgerstruktur, dann gibt es
genau eine bijektive Abbildung
eine Nachfolgerstruktur, dann gibt es
genau eine bijektive Abbildung
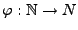 mit
mit
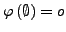 ,
,
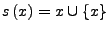 und
und
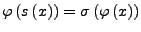
- Addition:
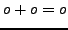
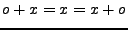
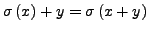
- Multiplikation:
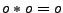
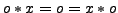

- Bei dieser Kodierung der natürlichen Zahlen gilt:
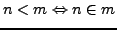
Das Peano-Axiom
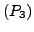 sagt: ist
sagt: ist 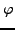 eine Aussage
über natürliche Zahlen und gilt:
eine Aussage
über natürliche Zahlen und gilt:
-
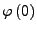 ist wahr
ist wahr
-
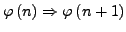
dann ist
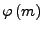 wahr für alle
wahr für alle
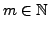 .
.





Next: Relationen
Up: Mengen, natürliche Zahlen, Induktion
Previous: Mengen
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]() mit einer Abbildung
mit einer Abbildung
![]() (
(![]() heiße Nachfolgerabbildung) heißt Nachfolgerstruktur,
falls sie die Peano-Axiome erfüllt:
heiße Nachfolgerabbildung) heißt Nachfolgerstruktur,
falls sie die Peano-Axiome erfüllt:
![]() sagt: ist
sagt: ist ![]() eine Aussage
über natürliche Zahlen und gilt:
eine Aussage
über natürliche Zahlen und gilt: