Für die Anzahl der Elemente einer Menge ![]() schreibe kurz:
schreibe kurz:
![]() (bzw.
(bzw.
![]() )
)
Wir schreiben für die Zahl ![]() dessen Fakultät
mit
dessen Fakultät
mit ![]() . Wir definieren
. Wir definieren ![]() und
und
![]() .
.
Der Binomialkoeffizient
![]() ,
lies
,
lies ![]() über
über ![]() , ist definiert für alle
, ist definiert für alle
![]() .
.
Sind
![]() Elemente eines Ringes. Dann setze
das Summensymbol wie folgt:
Elemente eines Ringes. Dann setze
das Summensymbol wie folgt:
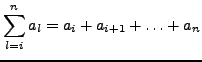
Sind sie sogar Elemente eines kommutativen Ringes setzen wir das Produktsymbol wie folgt:
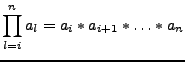
Sei ![]() eine
eine ![]() -elementige endliche Menge. Dann besitzt
-elementige endliche Menge. Dann besitzt ![]() genau
genau
![]() Teilmengen. Darunter sind genau
Teilmengen. Darunter sind genau
![]()
![]() -elementige Teilmengen.
-elementige Teilmengen.
Sind ![]() Elemente eines kommutativen Ringes, so gilt:
Elemente eines kommutativen Ringes, so gilt:
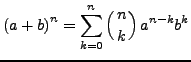
Sei ![]() ein Körper,
ein Körper, ![]() und
und ![]() . Dann gilt:
. Dann gilt:
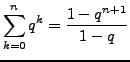
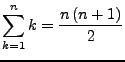
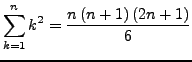
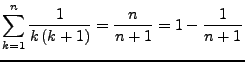
Eine Aussage gilt für fast alle natürlichen Zahlen, wenn sie nur endlich viele Ausnahmen hat.