Es sei
![]() eine unendliche Menge natürlicher Zahlen.
Eine (reelle) Folge ist eine Abbildung
eine unendliche Menge natürlicher Zahlen.
Eine (reelle) Folge ist eine Abbildung
![]() .
.
![]() ist die Indexmenge der Folge, die Zahlen
ist die Indexmenge der Folge, die Zahlen
![]() heißen Folgenglieder der Folge.
Schreibe auch
heißen Folgenglieder der Folge.
Schreibe auch
![]() .
.
Eine Folge
![]() konvergiert gegen
eine Zahl
konvergiert gegen
eine Zahl ![]() , falls es zu jedem
, falls es zu jedem
![]() ein
ein
![]() gibt, so dass
gibt, so dass
![]() für alle
für alle ![]() mit
mit ![]() gilt. Mit Quantoren ausgedrückt:
gilt. Mit Quantoren ausgedrückt:
Eine Folge mit dem Grenzwert 0 nennen wir Nullfolge.
Eine Folge
![]() heißt beschränkt,
falls es Zahlen
heißt beschränkt,
falls es Zahlen
![]() gibt mit
gibt mit
![]() für alle
für alle ![]() . Äquivalent dazu: Es gibt ein
. Äquivalent dazu: Es gibt ein
![]() mit
mit
![]() für alle
für alle ![]() .
.
Jede konvergente Folge ist beschränkt.
Eine Folge
![]() heißt
heißt
Ist die Folge
![]() monoton wachsend (fallend)
und beschränkt, dann konvergiert sie.
monoton wachsend (fallend)
und beschränkt, dann konvergiert sie.
Seien
![]() und
und
![]() konvergent mit
konvergent mit
![]() und
und
![]() .
Betrachte die Summenfolge
.
Betrachte die Summenfolge
![]() und Produktfolge
und Produktfolge
![]() .
Es gilt
.
Es gilt
Falls
![]() für alle
für alle ![]() gilt, folgt
gilt, folgt
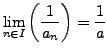
Eine Zahl ![]() heißt Häufungspunkt der
Folge
heißt Häufungspunkt der
Folge
![]() , falls für jedes
, falls für jedes
![]() die Menge
die Menge
![]() unendlich ist.
unendlich ist.
Ist
![]() eine Folge, und ist
eine Folge, und ist
![]() unendlich, so heißt die Folge
unendlich, so heißt die Folge
![]() Teilfolge
der urspünglichen Folge.
Teilfolge
der urspünglichen Folge.
Jede beschränkte Folge auf einem Ring / Körper der die Supremumseigenschaft
erfüllt (z.B.
![]() ) hat mindestens einen Häufungspunkt.
) hat mindestens einen Häufungspunkt.
Der größte Häufungspunkt der beschränkten Folge
![]() nennt man Limes superior:
nennt man Limes superior:
Der kleinste Häufungspunkt heißt Limes inferior: