




Next: Körper
Up: Ringe, Körper, Anordnung
Previous: Ringe, Körper, Anordnung
Contents
Index
Subsections
Gegeben sei eine Menge 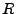 . Wir nehmen an, es gibt in
. Wir nehmen an, es gibt in 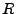 zwei spezielle
Elemente, die 0 (Null) und
zwei spezielle
Elemente, die 0 (Null) und 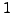 (Eins) heißen. Weiter
soll es auf
(Eins) heißen. Weiter
soll es auf 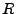 zwei Verknüpfungen ``
zwei Verknüpfungen ``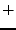 '' (plus) und ``
'' (plus) und ``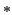 ''
(mal) geben, die jeweils zwei Elementen
''
(mal) geben, die jeweils zwei Elementen 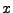 und
und 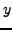 in
in 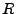 neue
Elemente
neue
Elemente 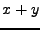 und
und 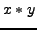 in
in 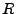 zuordnen. Wir nennen
zuordnen. Wir nennen
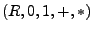 einen kommutativen Ring,
falls die folgenden Rechenregeln für alle
einen kommutativen Ring,
falls die folgenden Rechenregeln für alle 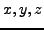 in
in 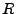 gelten.
gelten.
- Kommutativgesetze
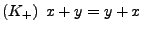
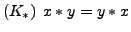
- Assoziativgesetze
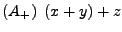 =
=
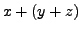
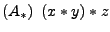 =
=
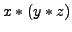
- Distributivgesetze
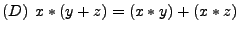
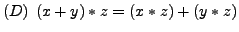
- Existens von Neutralelementen
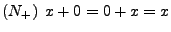
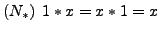
- Inverses Element
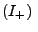 zu jedem
zu jedem 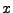 gibt es genau ein
gibt es genau ein 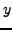 mit
mit 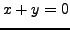 .
Schreibe
.
Schreibe 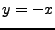
-
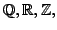 sind Beispiele für kommutative
Ringe.
sind Beispiele für kommutative
Ringe.
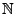 ist kein Ring.
ist kein Ring.
- Falls
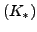 nicht ausdrücklich verlangt wird, spricht
man von einem nicht-kommutativen Ring.
nicht ausdrücklich verlangt wird, spricht
man von einem nicht-kommutativen Ring.
In einem kommutativen Ring gelten folgende Rechenregeln:
- Klammern werden nur geschrieben wenn sie nicht durch die Assoziativität
überflüssig gemacht werden.
-
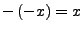
- aus
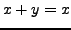 folgt
folgt 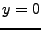
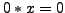
-
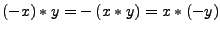





Next: Körper
Up: Ringe, Körper, Anordnung
Previous: Ringe, Körper, Anordnung
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]() . Wir nehmen an, es gibt in
. Wir nehmen an, es gibt in ![]() zwei spezielle
Elemente, die 0 (Null) und
zwei spezielle
Elemente, die 0 (Null) und ![]() (Eins) heißen. Weiter
soll es auf
(Eins) heißen. Weiter
soll es auf ![]() zwei Verknüpfungen ``
zwei Verknüpfungen ``![]() '' (plus) und ``
'' (plus) und ``![]() ''
(mal) geben, die jeweils zwei Elementen
''
(mal) geben, die jeweils zwei Elementen ![]() und
und ![]() in
in ![]() neue
Elemente
neue
Elemente ![]() und
und ![]() in
in ![]() zuordnen. Wir nennen
zuordnen. Wir nennen
![]() einen kommutativen Ring,
falls die folgenden Rechenregeln für alle
einen kommutativen Ring,
falls die folgenden Rechenregeln für alle ![]() in
in ![]() gelten.
gelten.