Next: Differentiation
Up: Integration
Previous: beschränkte Funktionen
Contents
Index
Subsections
Für eine Stufenfunktion 
bzgl. einer Zerlegung 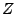
definieren wir das Integral folgendermaßen:
Eine beschränkte Funktion  heißt Regelfunktion,
falls es eine Folge von Stufenfunktionen
heißt Regelfunktion,
falls es eine Folge von Stufenfunktionen 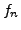 gibt, die gleichmäßig
gegen
gibt, die gleichmäßig
gegen  konvergiert. Wir sagen dann, diese Stufenfunktion approximiert
die Regelfunktion
konvergiert. Wir sagen dann, diese Stufenfunktion approximiert
die Regelfunktion  . Es sei
. Es sei
![$ R\left(\left[a,b\right],\mathbb{R}\right)<B\left(\left[a,b\right],\mathbb{R}\right)$](img695.png) die Menge aller Regelfunktionen.
die Menge aller Regelfunktionen.
-
![$ R\left(\left[a,b\right],\mathbb{R}\right)$](img696.png) ist ein (Folgen-)Vollständiger
normierter Vektorraum (bzgl.
ist ein (Folgen-)Vollständiger
normierter Vektorraum (bzgl.
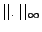 )
)
- falls
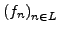 und
und
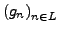 Folgen in
Folgen in
![$ \textrm{Step}\left(\left[a,b\right],\mathbb{R}\right)$](img699.png) ,
die die gleiche Regelfunktion approximieren, so gilt
,
die die gleiche Regelfunktion approximieren, so gilt
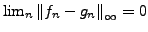
- Alle stetigen Funktionen auf endlich abgeschlossenen Intervallen sind
Regelfunktionen:
![$ C\left(\left[a,b\right],\mathbb{R}\right)\subsetneq R\left(\left[a,b\right],\mathbb{R}\right)$](img701.png)
- Ist ein Ring bzg. Addition und Multiplikation.
Integral allgemein
Ist  eine Regelfunktion und
eine Regelfunktion und
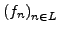 eine
Folge von Stufenfunktionen, die gleichmäßig gegen
eine
Folge von Stufenfunktionen, die gleichmäßig gegen  konvergiert.
Wir setzen
konvergiert.
Wir setzen
- Dieser Grenzwert existiert
- Ist unabhängig von der konkreten Wahl der Stufenfunktion
- Dieser Ausdruck heißt Riemann-Integral
von
 , es gibt noch weitere Integraldefinitionen
, es gibt noch weitere Integraldefinitionen
- Sind
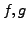 Regelfunktionen mit
Regelfunktionen mit
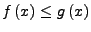 für alle
für alle
![$ x\in\left[a,b\right]$](img704.png) , so gilt
, so gilt
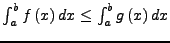
Die Menge
nennt sich eine äquidistante
Zerlegung der Intervalls
![$ \left[a,b\right]$](img669.png) . Sei
. Sei
![$ f:\left[a,b\right]\rightarrow\mathbb{R}$](img514.png) eine stetige Funktion. Die Funktionsfolge
von Stufenfunktionen konvergiert gleichmäßig gegen
eine stetige Funktion. Die Funktionsfolge
von Stufenfunktionen konvergiert gleichmäßig gegen  , d.h.
, d.h.
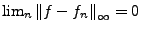 .
.
Das Integral ist hiermit also:
- Dies ist keine praktikabele Methode zum symbolischen errechnen
des Integrals, aber es ist eine Basis für numerische Verfahren.
- für manche Funktionen können auch andere Zerlegungen von Vorteil sein
Sei
![$ f,g\in R\left(\left[a,b\right],\mathbb{R}\right)$](img709.png) und
und
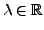 .
Dann gilt:
.
Dann gilt:
Mittelwertsatz (MWS) der Integralrechnung
Sei
![$ p\in R\left(\left[a,b\right],\mathbb{R}\right)$](img715.png) und
und
![$ f\in C\left(\left[a,b\right],\mathbb{R}\right)$](img716.png) und es gelte
und es gelte
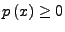 für alle
für alle
![$ x\in\left[a,b\right]$](img704.png) .
Dann gibt es
.
Dann gibt es
![$ t\in\left[a,b\right]$](img718.png) mit
mit
-
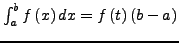 mit
mit
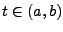
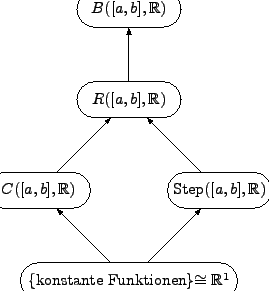
- Die Pfeile
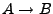 deuten an, dass
deuten an, dass 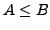 (
(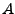 ein Untervektrorraum
von
ein Untervektrorraum
von 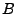 ist)
ist)
-
![$ \left\{ \textrm{konstante Funktionen}\right\} =C\left(\left[a,b\right],\mathbb{R}\right)\cap\textrm{Step}\left(\left[a,b\right],\mathbb{R}\right)$](img725.png)
- Bis auf den Raum der konstanten Funktionen sind dies alles unendlichdimensionale
Vektorräume
- Zwischen
![$ B\left(\left[a,b\right],\mathbb{R}\right)$](img726.png) und
und
![$ R\left(\left[a,b\right],\mathbb{R}\right)$](img696.png) liegen noch weitere integrierbare Funktionen, allerdings mit anderen
Integraldefinitionen.
liegen noch weitere integrierbare Funktionen, allerdings mit anderen
Integraldefinitionen.
- Alle Vektorräume bis auf
![$ \textrm{Step}\left(\left[a,b\right],\mathbb{R}\right)$](img699.png) sind vollständig bezüglich
sind vollständig bezüglich
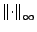





Next: Differentiation
Up: Integration
Previous: beschränkte Funktionen
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]()
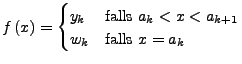
![]()
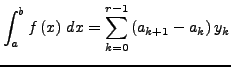
![]() heißt Regelfunktion,
falls es eine Folge von Stufenfunktionen
heißt Regelfunktion,
falls es eine Folge von Stufenfunktionen ![]() gibt, die gleichmäßig
gegen
gibt, die gleichmäßig
gegen ![]() konvergiert. Wir sagen dann, diese Stufenfunktion approximiert
die Regelfunktion
konvergiert. Wir sagen dann, diese Stufenfunktion approximiert
die Regelfunktion ![]() . Es sei
. Es sei
![]() die Menge aller Regelfunktionen.
die Menge aller Regelfunktionen.
![]() eine Regelfunktion und
eine Regelfunktion und
![]() eine
Folge von Stufenfunktionen, die gleichmäßig gegen
eine
Folge von Stufenfunktionen, die gleichmäßig gegen ![]() konvergiert.
Wir setzen
konvergiert.
Wir setzen
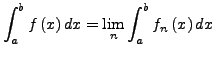
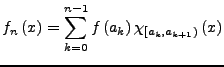
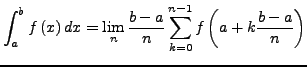
![]() und
und
![]() .
Dann gilt:
.
Dann gilt:
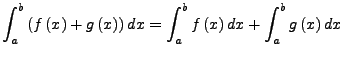
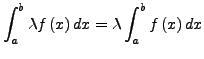
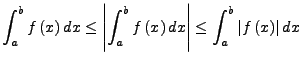
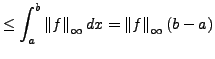
![]() und
und
![]() und es gelte
und es gelte
![]() für alle
für alle
![]() .
Dann gibt es
.
Dann gibt es
![]() mit
mit