Metrische Räume

Metrik / Metrischer Raum

Sei $X$ eine Menge, $d:X\times X\rightarrow\mathbb{R}$ eine Abbildung. Wir nennen $d$ eine Metrik (mathematischer Term für ``Abstandsbegriff'') und $\left(X,d\right)$ einen metrischen Raum, falls für alle $u,v,w\in X$ gilt:

1. $\left(M1\right)$ $d\left(u,v\right)=d\left(v,u\right)\ge0$
   die Metrik ist positiv und symmetrisch
2. $\left(M2\right)$ $d\left(u,v\right)=0\Leftrightarrow u=v$
3. $\left(M3\right)$ $d\left(u,w\right)\le d\left(u,v\right)+d\left(v,w\right)$
   Dreiecksungleichung

• $X=\mathbb{R}$ $d\left(u,v\right)=\left\vert u-v\right\vert$ ist ein metrischer Raum
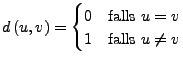• $X$ belibige Menge mit $X\neq\emptyset$ und $d\left(u,v\right)=\begin{cases} 0 & \textrm{falls }u=v\\ 1 & \textrm{falls }u\neq v\end{cases}$ ist ein metrischer Raum, mit der diskreten Metrik.
• $X=\mathbb{R}^{2}=\left\{ \left(u_{1},u_{2}\right)\vert u_{1},u_{2}\in\mathbb{R}\right\}$, $d\left(\left(u_{1},u_{2}\right),\left(v_{1},v_{2}\right)\right)=\left\vert u_{1}-v_{1}\right\vert+\left\vert u_{2}-v_{2}\right\vert$ ist ein metrischer Raum mit der Manhattan-Taxi-Metrik.
• Unterraum
  Ist $\left(X,d\right)$ ein metrischer Raum, und ist $A\subseteq X,$ dann ist der Unterraum $\left(A,d\right)$ ebenfalls ein metrischer Raum.

offene Kugel

Sei $\left(X,d\right)$ metrischer Raum, $r>0$ und $x\in X$. Die Menge

$$B_{r}\left(X\right)=\left\{ u\in X\vert d\left(u,x\right)<r\right\}$$

heißt offene $r$-Kugel um $x$.

Folgen und Konvergenz

Sei $J\subseteq\mathbb{N}$ unendliche Menge, $\left(X,d\right)$ ein metrischer Raum. Eine Folge, $\left(x_{j}\right)_{j\in J}$ ist eine Abbildung $J\rightarrow X,$ $j\mapsto x_{j}$. Schreibe kurz $\left(x_{j}\right)_{j\in J}\subseteq X$ dafür.

Die Folge $\left(x_{j}\right)_{j\in J}$ konvergiert gegen $x\in X$, falls gilt: zu jedem $\varepsilon>0$ gibt es $N\in\mathbb{N}$ so, dass für alle $k\ge N$ gilt $d\left(x_{k},x\right)\le\varepsilon$.

$$\forall\varepsilon>0:\exists N\in\mathbb{N}:\forall k\ge N:d\left(x_{k},x\right)\le\varepsilon$$

• Für $X=\mathbb{R}$, $d\left(u,v\right)=\left\vert u-v\right\vert$ ist dies genau die Definition aus sub:Konvergenz in R^1.
• Lässt sich auch so schreiben:
  Die Folge konvergiert genau dann gegen $x$, falls es zu jedem $r>0$ ein $N\in\mathbb{N}$ gibt, so dass $x_{k}\in B_{r}\left(x\right)$ für alle $k\ge N$.
  $$\forall r>0:\exists N\in\mathbb{N}:\forall k\ge N:x_{k}\in B_{r}\left(x\right)$$

• Eine Folge hat genau eine Zahl:
  Sei $\left(X,d\right)$ metrischer Raum, $\left(x_{j}\right)_{j\in J}$ Folge. Falls die Folge gegen $x\in X$ und gegen $y\in X$ konvergiert, so gilt $x=y$.
• Konvergente Folgen auf Räumen mit einer diskreten Metrik sind für fast alle Folgenglieder konstant.

Cauchy-Folge

$\left(CF\right)$ Es sei $\left(x_{j}\right)_{j\in J}$ eine Folge in einem metrischen Raum $\left(X,d\right)$. Wir sagen, $\left(x_{j}\right)_{j\in J}$ ist eine Cauchy-Folge falls gilt: zu jedem $\varepsilon>0$ gibt es $N\in\mathbb{N}$, so dass $d\left(x_{l},x_{m}\right)\le\varepsilon$ für alle $l,m\ge N$.

$$\forall\varepsilon>0:\exists N\in\mathbb{N}:\forall l,m\ge N:d\left(x_{l},x_{m}\right)\le\varepsilon$$

• Jede konvergente Folge in $\left(X,d\right)$ ist eine Cauchy-Folge. Umgekehrt nicht umbedingt.

Vollständigkeit

Ein metrischer Raum $\left(X,d\right)$ heißt vollständig falls jede Cauchy-Folge $\left(x_{j}\right)_{j\in J}$ einen Grenzwert $x\in X$ hat.

• Vollständigkeit vererbt sich nicht unbedingt auf Teilmengen.

abgeschlossen

Eine Teilmenge $A\subseteq X$ eines metrischen Raumes $\left(X,d\right)$ heißt abgeschlossen, wenn für jede Folge von Elementen $\left(a_{j}\right)_{j\in J}\subseteq A$ mit Grenzwert $x\in X$ gilt $x\in A$.

• $\emptyset$ und $X$ sind immer abgeschlossen in $\left(X,d\right)$
• Abgeschlossenheit ist immer relativ zu einem metrischen Raum zu sehen
• Vereinigungen endlich vieler abgeschlossener Teilmengen in $X$ sind abgeschlossen
• Durchschnitte beliebig vieler abgeschlossener Teilmengen in $X$ sind abgeschlossen
• Eine vollständige Teilmenge ist immer auch abgeschlossen.
• Sei $\left(X,d\right)$ ein vollständiger metrischer Raum. Dann gilt: $A\subseteq X$ ist abgeschlossen genau dann, wenn $\left(A,d\right)$ vollständig ist.

topologische Äquivalenz

Seien $\left(X,d\right)$ und $\left(X,h\right)$ metrische Räume. Wenn für alle Folgen $\left(a_{j}\right)_{j\in J}$ in $X$ folgendes gilt, werden $h$ und $d$ topologisch äquivalent genannt: $\left(a_{j}\right)_{j\in J}$ konvergiert genau dann bezüglich $\left(X,d\right)$, wenn $\left(a_{j}\right)_{j\in J}$ bezüglich $\left(X,h\right)$ konvergiert.

• dies ist eine Äquivalenzrelation
• Siehe auch sub:=C4quivalenz-von-Normen.

Segmente

Sei $\left(X,d\right)$ ein metrischer Raum. Das Segment in $X$ zwischen $x,z\in X$ ist die Menge aller Punkte für die die Dreiecksungleichung scharf ist, also

$$\left[x,z\right]=\left\{ y\in X\vert d\left(x,z=d\left(x,y\right)+d\left(y,z\right)\right)\right\}$$

• Mit Betrag (Standardmetrik) als $d$ und $\mathbb{R}$ als $X$ ist dies genau das abgeschlossene Intervall zwischen $x$ und $z$

Abschneiden einer Metrik

Sei $\left(X,d\right)$ ein metrischer Raum. Die Abbildung $d':X\times X\rightarrow\mathbb{R}:\left(x,y\right)\mapsto\min\left\{ 1,d\left(x,y\right)\right\}$ ist wieder eine Metrik. $d$ und $d'$ sind topologisch äquivalent.