Sei ![]() ein reeller Vektorraum (über dem Körper
ein reeller Vektorraum (über dem Körper
![]() ) (belibiger
Dimension - auch unendlich). Eine Norm auf
) (belibiger
Dimension - auch unendlich). Eine Norm auf ![]() ist eine Abbildung
ist eine Abbildung
![]() mit folgenden Eigenschaften für alle
mit folgenden Eigenschaften für alle ![]() und alle
und alle
![]() :
:
Sei
![]() und
und
![]() .
.
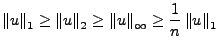
Ein Banach-Raum ist ein vollständiger normierter Raum.
Sei ![]() ein reeller Vektorraum,
ein reeller Vektorraum,
![]() eine Abbildung. Falls gilt:
eine Abbildung. Falls gilt:
Falls zusätzlich gilt:
![]() für
alle
für
alle ![]() , so heißt
, so heißt ![]() symmetrische Bilinearform.
symmetrische Bilinearform.
Wenn ![]() symmetrisch ist, und wenn
symmetrisch ist, und wenn
![]() ist für
alle
ist für
alle ![]() , so heißt
, so heißt ![]() inneres Produkt.
inneres Produkt.
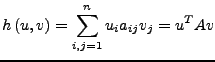
Sei ![]() ein reeller Vektroraum,
ein reeller Vektroraum, ![]() ein inneres Produkt. Setze
ein inneres Produkt. Setze
![]() ,
das ist eine Norm auf
,
das ist eine Norm auf ![]() .
.
Sei
![]() eine Norm auf
eine Norm auf ![]() . Falls es hierzu
ein inneres Produkt gibt, lässt es sich wie folgt beschreiben:
. Falls es hierzu
ein inneres Produkt gibt, lässt es sich wie folgt beschreiben:
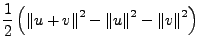 |
|||
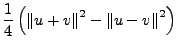 |
Ist ![]() ein inneres Produkt auf
ein inneres Produkt auf ![]() , so gilt
, so gilt
Die klassische Form lautet
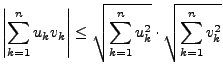
Ist h ein inneres Produkt auf ![]() , und ist V in der zugehörigen Metrik
vollständig, dann heißt
, und ist V in der zugehörigen Metrik
vollständig, dann heißt
![]() reeller Hilber-Raum.
reeller Hilber-Raum.
Sei
![]() der Raum aller Folgen
der Raum aller Folgen
![]() in
in
![]() mit folgender Eigenschaft:
mit folgender Eigenschaft:
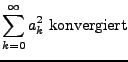
Dies sind die quadratisch summierbaren Folgen. Das innere Produkt ist wie folgt definiert
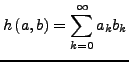
Dies ist ein unendlich dimensionaler Hilbert-Raum.
Sei ![]() ein Normierter Vektorraum.
ein Normierter Vektorraum.
![]() wird
genau dann von einem Inneren Produkt induziert, wenn die Parallelogrammgleichung
gilt
wird
genau dann von einem Inneren Produkt induziert, wenn die Parallelogrammgleichung
gilt