Seien
![]() und
und
![]() metrische
Räume,
metrische
Räume,
![]() eine Abbildung. Wir sagen
eine Abbildung. Wir sagen ![]() ist
stetig in
ist
stetig in ![]() , falls folgendes gilt:
, falls folgendes gilt:
Für jede Folge
![]() in
in ![]() mit Grenzwert
mit Grenzwert
![]() soll gelten
soll gelten
![]() :
:
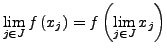
Falls ![]() in jedem Punkt
in jedem Punkt ![]() stetig ist, so heißt
stetig ist, so heißt ![]() stetig. Es sei
stetig. Es sei
![]()
Eine Funktion
![]() zwischen Metrischen Räumen heißt
L-Lipschitz-stetig
für
zwischen Metrischen Räumen heißt
L-Lipschitz-stetig
für
![]() , falls
, falls
![]() für alle
für alle ![]() .
.
Sind
![]() ,
,
![]() ,
,
![]() metrische Räume,
metrische Räume,
![]() und
und
![]() ,
, ![]() stetig. Dann ist auch
stetig. Dann ist auch
![]() stetig.
stetig.
Ist
![]() ein metrischer Raum, so ist
ein metrischer Raum, so ist
![]() ein Vektorraum und ein Ring. Für
ein Vektorraum und ein Ring. Für
![]() ,
,
![]() sind folgende Funktionen wieder stetig:
sind folgende Funktionen wieder stetig:
Eine Abbilung
![]() zwischen den metrischen Räumen
zwischen den metrischen Räumen
![]() und
und
![]() ist stetig in
ist stetig in ![]() genau dann, wenn
gilt: Zu jedem
genau dann, wenn
gilt: Zu jedem
![]() gibt es ein ein
gibt es ein ein ![]() , so dass
aus
, so dass
aus
![]() folgt
folgt
![]() .
.
Dies ist äquivalten zu: ![]() ist genau dann stetig in
ist genau dann stetig in ![]() , wenn
es für jede offene
, wenn
es für jede offene
![]() -Kugel
-Kugel
![]() um
um
![]() eine offene
eine offene ![]() -Kugel
-Kugel
![]() um
um ![]() mit
mit
![]() gibt.
gibt.