




Next: endlichdimensionale Räume
Up: Stetige Funktionen
Previous: Stetige Funktionen
Contents
Index
Subsections
Seien
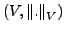 und
und
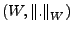 normierte Räume, sei
normierte Räume, sei
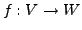 linear. Die folgenden Aussagen
sind äquivalent.
linear. Die folgenden Aussagen
sind äquivalent.
 ist stetig
ist stetig
- Es existiert ein
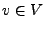 so dass
so dass  in
in 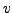 stetig ist
stetig ist
 ist
ist 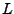 -Lipschitzstetig für eine Zahl
-Lipschitzstetig für eine Zahl 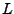
- Es gibt eine Zahl
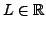 so, dass
so, dass
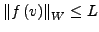 für alle
für alle 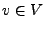 mit
mit
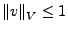 .
.
Es sei
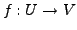 eine lineare stetige Abbildung zwischen
normierten Räumen. Wir definieren die Operatornorm
von
eine lineare stetige Abbildung zwischen
normierten Räumen. Wir definieren die Operatornorm
von  durch
durch
Die Menge
ist ein Vektorraum, und die Operratornorm
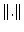 ist eine Norm darauf.
ist eine Norm darauf.
-
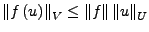 gilt für alle
gilt für alle 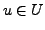 .
.
- Die kleinste Lipschitzkonstante ist die Operatornorm
- Wenn
 symmetrisch und
symmetrisch und 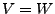 dann gilt
dann gilt
Sein
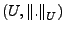 und
und
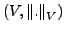 normierte Räume, und ist
normierte Räume, und ist 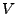 vollständig (d.h. Banachraum), so ist
vollständig (d.h. Banachraum), so ist
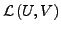 auch vollständig.
auch vollständig.
- Für alle
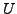 ist
ist
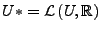 ein Banachraum.
Diesen Raum nennt man auch Dualraum von
ein Banachraum.
Diesen Raum nennt man auch Dualraum von 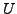 .
.
endlichdimensionale Vektorräume
Sei
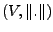 ein normierter Vektorraum,
ein normierter Vektorraum,
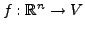 sei linear. Dann ist
sei linear. Dann ist  stetig
bezgl. der
stetig
bezgl. der
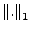 -Norm auf
-Norm auf
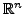 .
.
- siehe auch sub:Lipschitzstetigkeit-einer-endlichdimensionalen





Next: endlichdimensionale Räume
Up: Stetige Funktionen
Previous: Stetige Funktionen
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]() und
und
![]() normierte Räume, sei
normierte Räume, sei
![]() linear. Die folgenden Aussagen
sind äquivalent.
linear. Die folgenden Aussagen
sind äquivalent.
![]() eine lineare stetige Abbildung zwischen
normierten Räumen. Wir definieren die Operatornorm
von
eine lineare stetige Abbildung zwischen
normierten Räumen. Wir definieren die Operatornorm
von ![]() durch
durch
![]() und
und
![]() normierte Räume, und ist
normierte Räume, und ist ![]() vollständig (d.h. Banachraum), so ist
vollständig (d.h. Banachraum), so ist
![]() auch vollständig.
auch vollständig.
![]() ein normierter Vektorraum,
ein normierter Vektorraum,
![]() sei linear. Dann ist
sei linear. Dann ist ![]() stetig
bezgl. der
stetig
bezgl. der
![]() -Norm auf
-Norm auf
![]() .
.