




Next: Offene Mengen, Offene Abbildungen,
Up: Stetige Funktionen
Previous: Lineare Abbildungen
Contents
Index
Subsections
Sei
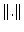 eine Norm auf
eine Norm auf
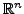 . Dann
gibt es eine Zahl
. Dann
gibt es eine Zahl 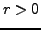 so, dass für alle
so, dass für alle
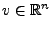 mit
mit
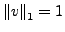 gilt
gilt
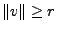 .
.
Sei
 eine Norm auf
eine Norm auf
 . Dann
ist die Identität
. Dann
ist die Identität
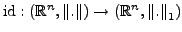 stetig.
stetig.
Seien
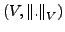 und
und
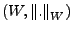 normierte Räume, sei
normierte Räume, sei
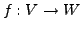 eine lineare Abbildung. Falls
eine lineare Abbildung. Falls
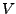 endliche Dimension hat, ist
endliche Dimension hat, ist 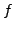 stetig.
stetig.
Lipschitzstetigkeit
einer endlichdimensionalen linearen Abbildung
Zu einer reellen 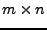 -Matrix
-Matrix
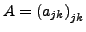 betrachten wir die ineare Abbildung
betrachten wir die ineare Abbildung
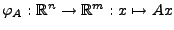 .
Mit
.
Mit
gilt, das
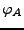 eine
eine 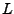 -Lipschitz-stetige Abbildung bezüglich
der
-Lipschitz-stetige Abbildung bezüglich
der 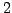 -Normen auf
-Normen auf
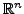 und
und
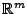 ist.
ist.
- siehe auch sub:linear_R^n_stetig
Äquivalenz von Normen
Sei 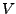 ein Vektorraum,
ein Vektorraum,
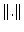 ,
,
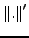 seien Normen auf
seien Normen auf 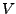 . Die Normen heißen äquivalent,
falls es Zahlen
. Die Normen heißen äquivalent,
falls es Zahlen
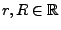 gibt, so dass
gibt, so dass
für alle 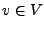 . Äquivalente Normen leifern den gleichen Konvergenzbegriff.
. Äquivalente Normen leifern den gleichen Konvergenzbegriff.
- Auf jedem endlich-dimensionalen Vektorraum sind alle Normen
äquivalent (z.B.
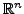 )
)
- Die entsprechenden Metrischen Räume sind also topologisch äquivalent.
Siehe auch sub:topologische-=C4quivalenz.
Ist
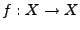 eine Abbildung und gilt
eine Abbildung und gilt
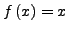 für ein
für ein 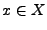 , so heißt
, so heißt 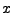 Fixpunkt
von
Fixpunkt
von 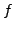 .
.
- Ist
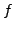 linear, so ist 0 ein Fixpunkt
linear, so ist 0 ein Fixpunkt
Banachs Fixpunktsatz
Sei
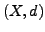 ein vollständiger metrischer Raum,
ein vollständiger metrischer Raum,
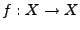 sei
sei 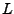 -Lipschitzstetig für ein
-Lipschitzstetig für ein 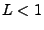 . Dann hat
. Dann hat 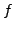 genau
einen Fixpunkt.
genau
einen Fixpunkt.
Genauer gilt: ist
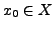 ein beliebiger Punkt,
ein beliebiger Punkt,
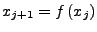 rekursiv, so gilt
rekursiv, so gilt
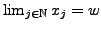 ist der gesuchte
Fixpunkt.
ist der gesuchte
Fixpunkt.
- Abschätzen des Fehlers bei Abbruch der Iteration an der
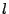 -ten Stelle
-ten Stelle
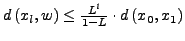
-
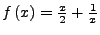 hat den Fixpunkt
hat den Fixpunkt 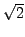





Next: Offene Mengen, Offene Abbildungen,
Up: Stetige Funktionen
Previous: Lineare Abbildungen
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]() eine Norm auf
eine Norm auf
![]() . Dann
gibt es eine Zahl
. Dann
gibt es eine Zahl ![]() so, dass für alle
so, dass für alle
![]() mit
mit
![]() gilt
gilt
![]() .
.
![]() eine Norm auf
eine Norm auf
![]() . Dann
ist die Identität
. Dann
ist die Identität
![]() stetig.
stetig.
![]() und
und
![]() normierte Räume, sei
normierte Räume, sei
![]() eine lineare Abbildung. Falls
eine lineare Abbildung. Falls
![]() endliche Dimension hat, ist
endliche Dimension hat, ist ![]() stetig.
stetig.
![]() -Matrix
-Matrix
![]() betrachten wir die ineare Abbildung
betrachten wir die ineare Abbildung
![]() .
Mit
.
Mit
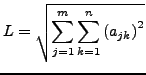
![]() ein Vektorraum,
ein Vektorraum,
![]() ,
,
![]() seien Normen auf
seien Normen auf ![]() . Die Normen heißen äquivalent,
falls es Zahlen
. Die Normen heißen äquivalent,
falls es Zahlen
![]() gibt, so dass
gibt, so dass
![]() eine Abbildung und gilt
eine Abbildung und gilt
![]() für ein
für ein ![]() , so heißt
, so heißt ![]() Fixpunkt
von
Fixpunkt
von ![]() .
.
![]() ein vollständiger metrischer Raum,
ein vollständiger metrischer Raum,
![]() sei
sei ![]() -Lipschitzstetig für ein
-Lipschitzstetig für ein ![]() . Dann hat
. Dann hat ![]() genau
einen Fixpunkt.
genau
einen Fixpunkt.
![]() ein beliebiger Punkt,
ein beliebiger Punkt,
![]() rekursiv, so gilt
rekursiv, so gilt
![]() ist der gesuchte
Fixpunkt.
ist der gesuchte
Fixpunkt.