




Next: Kurven
Up: Offene Mengen, Offene Abbildungen,
Previous: Offene Mengen, Offene Abbildungen,
Contents
Index
Subsections
Sei
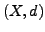 ein metrischer Raum. Eine Teilmenge
ein metrischer Raum. Eine Teilmenge
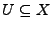 heißt offen in
heißt offen in 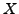 , falls gilt: zu jedem
, falls gilt: zu jedem 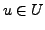 gibt es ein
gibt es ein
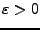 mit
mit
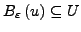 .
.
- Endliche Durchschnitte und beliebige Vereinigungen von Systemen offener
Mengen sind wieder offen
- Offene Intervalle auf
 sind offene Mengen
sind offene Mengen
-
 ist stets offen in
ist stets offen in 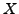
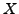 ist stets offen in
ist stets offen in 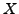
Eine Abbildung
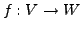 wird als offen
bezeichnet, falls für eine
wird als offen
bezeichnet, falls für eine
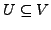 offen gilt das auch
offen gilt das auch
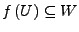 wieder offen ist.
wieder offen ist.
Eine Teilmenge
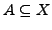 eines metrischen Raumes
eines metrischen Raumes
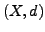 heißt abgeschlossen, wenn für jede Folge
von Elementen
heißt abgeschlossen, wenn für jede Folge
von Elementen
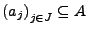 mit Grenzwert
mit Grenzwert
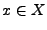 gilt
gilt 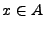 .
.
- Siehe auch sub:Vollst=E4ndigkeitR^n
Sei
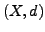 metrischer Raum,
metrischer Raum,
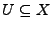 . Dann sind
gleichwertig:
. Dann sind
gleichwertig:
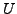 ist offen in
ist offen in 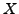
-
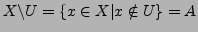 ist abgeschlossen
in
ist abgeschlossen
in 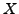
- Es gibt Mengen, die sowohl abgeschlossen als auch offen sind in
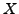 ,
z.B. sind sowohl
,
z.B. sind sowohl
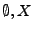 abgeschlossene als auch offene Mengen
in
abgeschlossene als auch offene Mengen
in 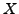
- Es gibt Mengen, die weder offen, noch abgeschlossen sind, z.B.
![$ \left(0,1\right]\subseteq\mathbb{R},\mathbb{Q}\subseteq\mathbb{R}$](img1095.png)
Seien
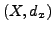 und
und
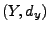 metrische
Räume,
metrische
Räume,
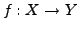 eine Abbildung. Dann sind äquivalent:
eine Abbildung. Dann sind äquivalent:
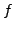 ist stetig
ist stetig
- für alle offenen
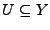 ist
ist
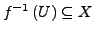 offen
offen
- für alle abgeschlossenen
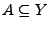 ist
ist
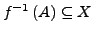 abgeschlossen
abgeschlossen
Für
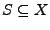 setzte
setzte
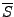 ist abgeschlossen und
ist abgeschlossen und
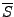 ist die kleinste
abgeschlossene Menge in
ist die kleinste
abgeschlossene Menge in 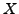 , die
, die 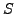 enthält.
enthält.
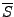 besteht
(abgesehen von
besteht
(abgesehen von
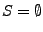 mit
mit
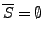 ) genau
aus den Grenzwerten konvergenter Folgen in
) genau
aus den Grenzwerten konvergenter Folgen in 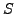 .
.
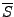 heißt
Abschluss von
heißt
Abschluss von 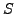 .
.
Wir betrachten einen metrischen Raum 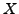 . Das Innere
. Das Innere
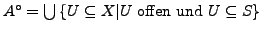 von
von 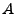 ist offen (das ist das offene Innere von
ist offen (das ist das offene Innere von 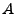 ).
).
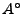 ist die größte offene Teilmenge von
ist die größte offene Teilmenge von 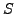 .
.
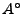 ist die Vereinigung aller offenen Teilmengen von
ist die Vereinigung aller offenen Teilmengen von 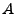
- Alternative Schreibweise:
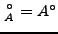
Wir betrachten einen metrischen Raum 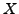 . Der Rand
. Der Rand
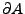 einer Menge
einer Menge 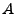 ist die Menge aller Punkte
ist die Menge aller Punkte 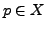 für die jede offene
für die jede offene
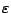 -Kugel
-Kugel
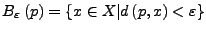 sowol Elemente aus
sowol Elemente aus 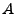 als auch Elemente aus
als auch Elemente aus
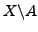 enthält.
enthält.
Ein Metrischer Raum
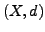 heißt kompakt,
falls jede Folge
heißt kompakt,
falls jede Folge
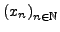 in
in 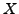 eine
konvergente Teilfolge hat.
eine
konvergente Teilfolge hat.
- In
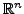 ist eine Teilmenge
ist eine Teilmenge 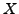 genau dann kompakt wenn
sie abgeschlossen und beschränkt bzgl.
genau dann kompakt wenn
sie abgeschlossen und beschränkt bzgl.
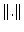 ist
ist
- Sei
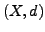 ein metrischer Raum, und
ein metrischer Raum, und
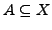 ist
kompakt, dann ist
ist
kompakt, dann ist 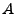 abgeschlossen und beschränkt
abgeschlossen und beschränkt
- Es sei
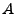 eine abgeschlossene Teilmenge von einem kompakten Raum
eine abgeschlossene Teilmenge von einem kompakten Raum
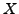 , dann ist
, dann ist 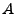 kompakt
kompakt
- Es sei
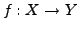 eine stetige Abbildung, dann ist das Bild
eine stetige Abbildung, dann ist das Bild
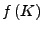 einer kompakten Menge
einer kompakten Menge
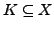 wieder kompakt
wieder kompakt
- Jede stetig differenzierbare reellwertige Funktion
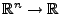 auf
einer kompakten Teilmenge
auf
einer kompakten Teilmenge
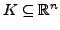 ist Lipschitz-stetig
ist Lipschitz-stetig
- Das Kreuzprodukt von abgeschlossenen Intervallen ist kompakt:
![$ \left[a_{1},b_{1}\right]\times\ldots\times\left[a_{n},b_{n}\right]\subseteq\mathbb{R}^{n}$](img1122.png) ist kompakt
ist kompakt
Sei
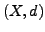 metrischer Raum und vollständig, sei
metrischer Raum und vollständig, sei
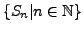 eine Menge von abgeschlossenen Teilmengen in
eine Menge von abgeschlossenen Teilmengen in 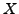 . Falls
. Falls
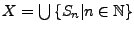 ,
so gibt es ein
,
so gibt es ein
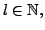 ein
ein 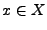 und ein
und ein
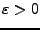 so, dass
so, dass
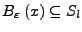 (d.h.
(d.h.
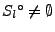 ).
).
Seien
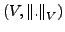 und
und
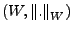 Banachräume,
Banachräume,
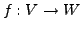 sei linear, stetig und surjektiv.
Dann ist
sei linear, stetig und surjektiv.
Dann ist 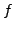 offen.
offen.
Ist
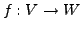 stetig, linear und bijektiv, dann ist
stetig, linear und bijektiv, dann ist 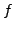 offen.
offen.
Sei 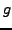 die Umkehrabbildung von
die Umkehrabbildung von 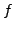 ,
dann ist
,
dann ist 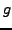 linear und stetig.
linear und stetig.
Es sei 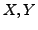 metrische Räume,
metrische Räume,
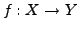 eine Abbildung.
Dann sind folgende Aussagen äquivalent:
eine Abbildung.
Dann sind folgende Aussagen äquivalent:
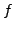 ist stetig
ist stetig
- Das Urbild
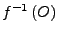 jeder offenen Menge
jeder offenen Menge
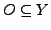 ist wieder offen
ist wieder offen
- Das Urbild
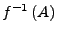 jeder abgeschlossenen Menge
jeder abgeschlossenen Menge
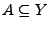 ist wieder abgeschlossen
ist wieder abgeschlossen
-
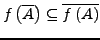 für
alle Teilmengen
für
alle Teilmengen
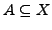
-
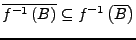 für alle Teilmengen
für alle Teilmengen
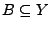





Next: Kurven
Up: Offene Mengen, Offene Abbildungen,
Previous: Offene Mengen, Offene Abbildungen,
Contents
Index
Marco Möller 14:31:11 17.12.2005
![]() ein metrischer Raum. Eine Teilmenge
ein metrischer Raum. Eine Teilmenge
![]() heißt offen in
heißt offen in ![]() , falls gilt: zu jedem
, falls gilt: zu jedem ![]() gibt es ein
gibt es ein
![]() mit
mit
![]() .
.
![]() wird als offen
bezeichnet, falls für eine
wird als offen
bezeichnet, falls für eine
![]() offen gilt das auch
offen gilt das auch
![]() wieder offen ist.
wieder offen ist.
![]() eines metrischen Raumes
eines metrischen Raumes
![]() heißt abgeschlossen, wenn für jede Folge
von Elementen
heißt abgeschlossen, wenn für jede Folge
von Elementen
![]() mit Grenzwert
mit Grenzwert
![]() gilt
gilt ![]() .
.
![]() metrischer Raum,
metrischer Raum,
![]() . Dann sind
gleichwertig:
. Dann sind
gleichwertig:
![]() und
und
![]() metrische
Räume,
metrische
Räume,
![]() eine Abbildung. Dann sind äquivalent:
eine Abbildung. Dann sind äquivalent:
![]() setzte
setzte
![]() . Das Innere
. Das Innere
![]() von
von ![]() ist offen (das ist das offene Innere von
ist offen (das ist das offene Innere von ![]() ).
).
![]() ist die größte offene Teilmenge von
ist die größte offene Teilmenge von ![]() .
.
![]() . Der Rand
. Der Rand
![]() einer Menge
einer Menge ![]() ist die Menge aller Punkte
ist die Menge aller Punkte ![]() für die jede offene
für die jede offene
![]() -Kugel
-Kugel
![]() sowol Elemente aus
sowol Elemente aus ![]() als auch Elemente aus
als auch Elemente aus
![]() enthält.
enthält.
![]() heißt kompakt,
falls jede Folge
heißt kompakt,
falls jede Folge
![]() in
in ![]() eine
konvergente Teilfolge hat.
eine
konvergente Teilfolge hat.
![]() metrischer Raum und vollständig, sei
metrischer Raum und vollständig, sei
![]() eine Menge von abgeschlossenen Teilmengen in
eine Menge von abgeschlossenen Teilmengen in ![]() . Falls
. Falls
![]() ,
so gibt es ein
,
so gibt es ein
![]() ein
ein ![]() und ein
und ein
![]() so, dass
so, dass
![]() (d.h.
(d.h.
![]() ).
).
![]() und
und
![]() Banachräume,
Banachräume,
![]() sei linear, stetig und surjektiv.
Dann ist
sei linear, stetig und surjektiv.
Dann ist ![]() offen.
offen.
![]() stetig, linear und bijektiv, dann ist
stetig, linear und bijektiv, dann ist ![]() offen.
offen.
![]() die Umkehrabbildung von
die Umkehrabbildung von ![]() ,
dann ist
,
dann ist ![]() linear und stetig.
linear und stetig.
![]() metrische Räume,
metrische Räume,
![]() eine Abbildung.
Dann sind folgende Aussagen äquivalent:
eine Abbildung.
Dann sind folgende Aussagen äquivalent: