Sei ![]() ein normierter Raum (z.B.
ein normierter Raum (z.B.
![]() ) mit euklidischer
Norm. Sei
) mit euklidischer
Norm. Sei
![]() ein Intervall (offen, abgeschlossen,
halboffen oder
ein Intervall (offen, abgeschlossen,
halboffen oder
![]() ). Ein Weg in
). Ein Weg in ![]() ist eine stetige Abbildung
ist eine stetige Abbildung
Eine Peano-Kurve ist eine Raumfüllende
Kurve
![]() . Sei
. Sei
![]() eine stetige
eine stetige ![]() -periodische
Funktion mit
-periodische
Funktion mit
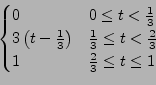 |
|||
Da ![]() auf
auf
![]() nicht benötigt wird spielt die Definiton
dort keine Rolle. Seien weiter
nicht benötigt wird spielt die Definiton
dort keine Rolle. Seien weiter
![]() und
und
![]() zwei (Koordinaten)-Funktionen
mit
zwei (Koordinaten)-Funktionen
mit
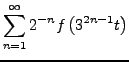 |
|||
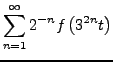 |
Dann ist
![]() eine
stetige und surjektive Abbildung.
eine
stetige und surjektive Abbildung.
Ein (metrischer) Raum ![]() heißt wegzusammenhängend, falls
sich je zwei Punkte
heißt wegzusammenhängend, falls
sich je zwei Punkte ![]() durch einen Weg in
durch einen Weg in ![]() verbinden
lassen.
verbinden
lassen.
Sei
![]() offenes Intervall,
offenes Intervall,
![]() eine Kurve,
eine Kurve,
![]() . Dann gibt es
. Dann gibt es
![]() so, dass
so, dass
![]() .
.
Falls es eine stetige Abbildung
![]() gibt, so dass
gibt, so dass
![]() gilt für
gilt für
![]() so heißt
so heißt
![]() Geschwindigkeit oder Tangentialvektor
der Kurve zur Zeit
Geschwindigkeit oder Tangentialvektor
der Kurve zur Zeit ![]() .
. ![]() ist somit in
ist somit in ![]() differenzierbar.
differenzierbar.
Falls ![]() in jedem
in jedem ![]() differenzierbar ist, heißt
differenzierbar ist, heißt ![]() differenzierbar, falls zusätzlich
differenzierbar, falls zusätzlich
![]() stetig ist, so heißt
stetig ist, so heißt ![]() stetig differenzierbar
oder
stetig differenzierbar
oder ![]() -Kurve.
-Kurve.
Ist
![]() ,
so ist
,
so ist ![]() genau dann (stetig) differenzierbar, wenn jedes einzelne
genau dann (stetig) differenzierbar, wenn jedes einzelne
![]() (stetig) differenzierbar ist, und
(stetig) differenzierbar ist, und
![]() .
.
Falls ![]()
![]() -Kurve ist, und falls
-Kurve ist, und falls ![]() (stetig) differenzierbar
ist, schreibe
(stetig) differenzierbar
ist, schreibe ![]() für die zweite Ableitung.
für die zweite Ableitung.
![]() heißt Beschleunigung zur Zeit
heißt Beschleunigung zur Zeit ![]() .
.
![]() offenes Intervall.
offenes Intervall.
Ist
![]() Kurve. Falls es ein
Kurve. Falls es ein ![]() gibt, eine (stetig) differenzierbare Kurve
gibt, eine (stetig) differenzierbare Kurve
![]() mit
mit
![]() für alle
für alle
![]() ,
so heißt
,
so heißt ![]() (stetig) differenzierbar auf
(stetig) differenzierbar auf
![]() , setze
, setze
![]() für
für
![]() .
.
Sei
![]() stetig differenzierbar. Die
Bogenlänge von
stetig differenzierbar. Die
Bogenlänge von ![]() ist
ist
![]() .
.
Ist
![]()
![]() -Kurve,
-Kurve,
![]() , ist
, ist
![]()
![]() -Funktion streng monoton
wachsend (d.h.
-Funktion streng monoton
wachsend (d.h.
![]() für alle
für alle ![]() ),
),
![]() mit
mit
![]() ,
,
![]() . Dann gilt
. Dann gilt