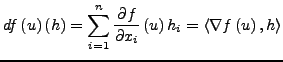Sei ![]() ein normierter Raum,
ein normierter Raum,
![]() offen, sei
offen, sei
![]() stetig. Sei
stetig. Sei
![]() . Wir sagen
. Wir sagen ![]() ist differenzierbar
im Punkt
ist differenzierbar
im Punkt ![]() , falls es
, falls es ![]() gibt, eine stetige Funktion
gibt, eine stetige Funktion
![]() ,
und eine stetige lineare Abbildung
,
und eine stetige lineare Abbildung
![]() , so
dass gilt:
, so
dass gilt:
![]() und
und
Dann heißt
![]() Ableitung
oder Differential von
Ableitung
oder Differential von ![]() in
in ![]() .
.
Falls ![]() in jedem Punkt
in jedem Punkt ![]() differenzierbar, so heißt
differenzierbar, so heißt ![]() differenzierbar, falls die Abbildung
differenzierbar, falls die Abbildung
Sei
![]() offen,
offen,
![]()
![]() -Funktion,
-Funktion,
![]() offen,
offen,
![]() stetig differenzierbare
Kurve mit
stetig differenzierbare
Kurve mit
![]() . Dann ist
. Dann ist
![]() mit
mit
Sei
![]() offen,
offen,
![]()
![]() -Funktion,
-Funktion,
![]() offen,
offen,
![]() reelle
Funktion mit
reelle
Funktion mit
![]() . Dann ist
. Dann ist
![]() mit
mit
Ist ![]() , so heißt
, so heißt
Sei
![]() ,
, ![]() . Dann ist
. Dann ist
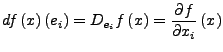
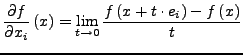
Sei
![]() offen,
offen,
![]() die Menge aller
stetig differenzierbaren Funktionen auf
die Menge aller
stetig differenzierbaren Funktionen auf ![]() . Das ist ein reeller
Vektorraum und ein Ring, also eine reelle Algebra. Es gilt:
. Das ist ein reeller
Vektorraum und ein Ring, also eine reelle Algebra. Es gilt:
Ist
![]() linear und stetig,
linear und stetig, ![]() , so ist
die Abbildung
, so ist
die Abbildung
![]() stetig differenzierbar,
und
stetig differenzierbar,
und
![]() .
.
Für
![]() offen,
offen,
![]()
![]() -Funktion
betrachte den Gradienten
-Funktion
betrachte den Gradienten
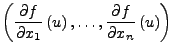 |
Das innere Produkt auf
![]() mit
mit
![]() .
Dann gilt:
.
Dann gilt:
Sei
![]() offen,
offen,
![]() stetig. Dann ist
stetig. Dann ist ![]() stetig differenzierbar genau dann, wenn alle
partiellen Ableitungen
stetig differenzierbar genau dann, wenn alle
partiellen Ableitungen
![]() existieren und stetig in
existieren und stetig in ![]() sind.
sind.
Für das Differential gilt dann