Seien ![]() normierte Räume,
normierte Räume,
![]() offen,
offen,
![]() stetig, sei
stetig, sei ![]() .
.
Wir sagen ![]() ist diferenzierbar in
ist diferenzierbar in
![]() , falls es eine lineare Abbildung
, falls es eine lineare Abbildung
![]() gibt, und
eine stetige Abbildung
gibt, und
eine stetige Abbildung
![]() mit
mit
![]() , so dass gilt
, so dass gilt
Falls ![]() in jedem Punkt
in jedem Punkt ![]() eine Ableitung hat, heißt
eine Ableitung hat, heißt ![]() differenzierbar. Falls zusätzlich die
Abbildung
differenzierbar. Falls zusätzlich die
Abbildung
Sei ![]() ein reeller normierter Vektorraum und seien
ein reeller normierter Vektorraum und seien
![]() und
und
![]() offen.
offen.
Ist
![]() linear und stetig,
linear und stetig,
![]() und
und
![]() . Damit ist
. Damit ist ![]()
![]() -Funktion mit Ableitung
-Funktion mit Ableitung
![]() .
.
Sei
![]() offen,
offen, ![]() normierte Räume,
normierte Räume,
![]() die Menge aller
die Menge aller ![]() Abbildungen von
Abbildungen von ![]() nach
nach ![]() .
.
Dann ist
![]() ein reeller Vektorraum. Es gilt für
alle
ein reeller Vektorraum. Es gilt für
alle
![]() und
und ![]()
Für
![]() ,
,
![]() offen und
offen und
![]() mit
mit
![]() .
Wenn
.
Wenn ![]()
![]() -Funktion ist, so auch
-Funktion ist, so auch
![]() mit
mit
![]() . Für die
Ableitung gilt dann mit
. Für die
Ableitung gilt dann mit
![]()
mit
![$\displaystyle \left[Df\left(u\right)\right]=\left(\begin{array}{ccc}
\frac{\par...
...f_{m}}{\partial x_{n}}\left(u\right)\end{array}\right)\in\mathbb{R}^{m\times n}$](img1295.png)
![]() wird als Jakobimatrix
von
wird als Jakobimatrix
von
![]() bezeichnet.
bezeichnet.
Sind ![]() normierte Räume,
normierte Räume,
![]() offen,
offen,
![]() offen,
offen,
![]() und
und
![]()
![]() -Funktionen
mit
-Funktionen
mit
![]() . Dann ist
. Dann ist
![]() ebenfalls
ebenfalls ![]() -Funktion und
-Funktion und
Ist
![]() offen,
offen,
![]()
![]() -Funktion.
Dann ist
-Funktion.
Dann ist
![]() stetig. Falls
stetig. Falls
![]() ebenfalls
ebenfalls ![]() -Funktion ist, heißt
-Funktion ist, heißt ![]() zweimal stetig
differenzierbar oder
zweimal stetig
differenzierbar oder ![]() -Funktion.
Schreibe
-Funktion.
Schreibe
![]() für die zweite Ableitung.
für die zweite Ableitung.
Entsprechend definiert man ![]() -mal stetig differenzierbare Funktionen,
-mal stetig differenzierbare Funktionen,
![]() -te Ableitung. Man erhält Vektorräume
-te Ableitung. Man erhält Vektorräume
![]() .
.
![]() sei ein Vektor und
sei ein Vektor und
![]() lineare Abbildung. Betrachte die zweite Ableitung
lineare Abbildung. Betrachte die zweite Ableitung
![]() .
.
Es gilt
![]() ist linear in
ist linear in ![]() uns
uns ![]() und somit eine bilineare Abbildung.
und somit eine bilineare Abbildung.
Für
![]() offen und
offen und
![]() gilt
gilt
![]() .
.
![]() offen,
offen,
![]() . Für
die zweite Ableitung gilt
. Für
die zweite Ableitung gilt
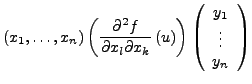 |
|||
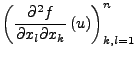 |
|||
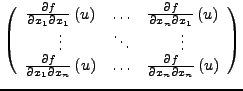 |
Ist
![]() offen,
offen,
![]() eine
eine ![]() -Funktion
und
-Funktion
und ![]() , so gilt
, so gilt
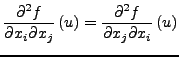
Sei
![]() offen,
offen,
![]() sei eine
sei eine ![]() -Funktion. Frage: gibt es
-Funktion. Frage: gibt es
![]() mit
mit
![]() ? Wenn ja, so heißt
? Wenn ja, so heißt ![]() Potential
zum Feld
Potential
zum Feld ![]() ).
).
Falls es ein Potential ![]() passend zu
passend zu ![]() gibt, gilt ist
gibt, gilt ist ![]() eine
eine
![]() -Funktion. Es muss also für
-Funktion. Es muss also für ![]() gelten
gelten
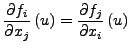
Im
![]() ist diese notwendige Bedingung äquivalent mit
Rotation von
ist diese notwendige Bedingung äquivalent mit
Rotation von ![]()
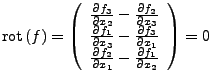
Falls ![]() sternförmig ist, sind diese
Bedingung nicht nur notwendig, sondern auch hinreichend.
sternförmig ist, sind diese
Bedingung nicht nur notwendig, sondern auch hinreichend.
Sternförmig bedeutet, das es einen ausgezeichneten Punkt im Raum gibt, von dem aus man alle anderen Punkte mit in der Menge liegenden Verbindungsgraden erreichen kann.