Sei ![]() ein Banachraum (= vollständiger normierter Raum),
ein Banachraum (= vollständiger normierter Raum),
![]() .
Eine Funktion
.
Eine Funktion
![]() heißt beschränkt,
falls die Menge
heißt beschränkt,
falls die Menge
![]() beschränkt ist. Sei
beschränkt ist. Sei
![]() die Menge aller beschränkter
Funktionen
die Menge aller beschränkter
Funktionen
![]() .
.
![]() ist ein reeller
Vektorraum. Setze
ist ein reeller
Vektorraum. Setze
![]() (Supremum von
(Supremum von ![]() ). Damit wird
). Damit wird
![]() ein normierter Vektorraum.
ein normierter Vektorraum.
Eine Funktion
![]() heißt Stufenfunktion,
falls es Zahlen
heißt Stufenfunktion,
falls es Zahlen
Der Abschluss von
![]() in
in
![]() besteht aus allen beschränkten Funktionen, die Grenzwerte (bzgl.
besteht aus allen beschränkten Funktionen, die Grenzwerte (bzgl.
![]() )
von Stufenfunktionen sind. Solche Funktionen heißen Regelfunktionen,
sie bilden einen Untervektorraum
)
von Stufenfunktionen sind. Solche Funktionen heißen Regelfunktionen,
sie bilden einen Untervektorraum
![]() .
Weil
.
Weil
![]() vollständig ist, ist
vollständig ist, ist
![]() ebenfalls vollständig.
ebenfalls vollständig.
Ist
![]() bzgl. Zerlegung
bzgl. Zerlegung
![]() ,
setze
,
setze
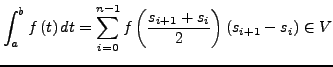
Für eine Regelfunktion
![]() , die Grenzwert einer Folge
, die Grenzwert einer Folge
![]() von Stufenfunktionen ist, setze
von Stufenfunktionen ist, setze
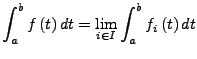
Ist
![]() linear und stetig, so gilt
linear und stetig, so gilt
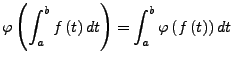
Im
![]() mit
mit
![]() und
und
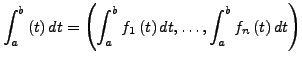
Sind ![]() Banachräume, dann gilt für
Banachräume, dann gilt für
![]() linear
und stetig
linear
und stetig
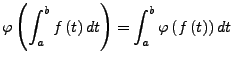
Insbesondere: Sind ![]() Banachräume,
Banachräume,
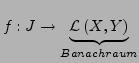 Regelfunktion, so gilt für jedes
Regelfunktion, so gilt für jedes ![]()
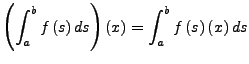
Ist
![]() stetig,
stetig,
![]() , so
ist
, so
ist
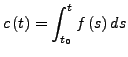
Seien ![]() Banachräume,
Banachräume,
![]() offen,
offen,
![]()
![]() -Abbildung. Sei
-Abbildung. Sei ![]() und
und ![]() so, dass
so, dass
![]() für alle
für alle
![]() . Dann gilt
. Dann gilt
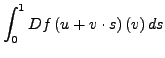 |
|||
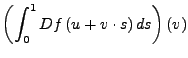 |