Sei ![]() ein Banachraum,
ein Banachraum,
![]() mit
mit
![]() .
Dann hat die lineare Abbildung
.
Dann hat die lineare Abbildung
![]() ein stetiges Inverses nämlich
ein stetiges Inverses nämlich
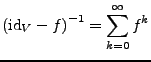
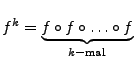 .
.
Sei ![]() ein Banachraum,
ein Banachraum,
Sei ![]() Banachräume,
Banachräume,
![]() offen
offen
![]()
![]() -Funktion,
-Funktion, ![]() . Falls
. Falls
![]() bijektiv ist, dann gibt es
bijektiv ist, dann gibt es ![]() eine
eine ![]() -Funktion
-Funktion
![]() ,
so dass
,
so dass
Sind ![]() Banachräume,
Banachräume,
![]() offen.
offen.
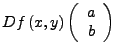 |
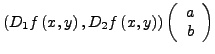 |
||
Seien ![]() Banachräume,
Banachräume,
![]() offen,
offen,
![]() sei
sei ![]() -Funktion, sei
-Funktion, sei
![]() .
.
Falls
![]() ein Isomorphismus ist,
so gibt es
ein Isomorphismus ist,
so gibt es
![]() offen,
offen,
![]()
![]() -Funktion mit
-Funktion mit
![]() , so dass
, so dass
![]() gilt für alle
gilt für alle
![]() .
.
Ist
![]() symmetrisch (d.h.
symmetrisch (d.h. ![]() ), so
gibt es eine Orthonormalbasis
), so
gibt es eine Orthonormalbasis
![]() des
des
![]() aus Eigenvektoren von
aus Eigenvektoren von ![]() . Bzgl. dieser Basis hat
. Bzgl. dieser Basis hat ![]() also Diagonalgestalt
mit den Eigenwerten auf der Diagonalen.
also Diagonalgestalt
mit den Eigenwerten auf der Diagonalen.
Sei
![]() differenzierbare Funktion,
differenzierbare Funktion,
![]() ebenfalls differenzierbar und es gelte
ebenfalls differenzierbar und es gelte
![]() für alle
für alle ![]() . An allen anderen Punkten
. An allen anderen Punkten
![]() an denen
an denen
![]() invertierbar ist gilt
invertierbar ist gilt