Sei
![]() Hilbertraum (d.h.
Hilbertraum (d.h. ![]() ist Vollständig, bzgl
Norm
ist Vollständig, bzgl
Norm
![]() ). Eine Teilmenge
). Eine Teilmenge
![]() ,
,
![]() heißt Orthonormalsystem
(ONS), falls
heißt Orthonormalsystem
(ONS), falls
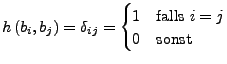
Ein ONS heißt vollständig, fallss der von
![]() erzeugte Unterraum
erzeugte Unterraum
![]() dicht
ist, d.h. falls
dicht
ist, d.h. falls
![]() .
.
ISt ![]() und ist
und ist ![]() vollständiges ONS, so heißen die Zahlen
vollständiges ONS, so heißen die Zahlen
![]() Fourierkoeffizienten
von
Fourierkoeffizienten
von ![]() . Für
. Für
![]() konvergiert dann
konvergiert dann
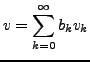
Sei
![]() und
und
![]() ist inneres Produkt auf
ist inneres Produkt auf ![]() . Leider ist
. Leider ist ![]() kein Hilbertraum,
aber er lässt sich zu einem Hilbertraum
kein Hilbertraum,
aber er lässt sich zu einem Hilbertraum
![]() vervollständigen (Dafür würde man einen anderen Integralbegriff benötigen).
vervollständigen (Dafür würde man einen anderen Integralbegriff benötigen).
Betrachte
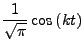 |
|||
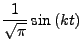 |
Die Menge
![]() ist ein vollständiges
ONS.
ist ein vollständiges
ONS.
Für
![]() (insbesondere für
(insbesondere für ![]() ) betrachte die Fourierkoeffizienten
) betrachte die Fourierkoeffizienten
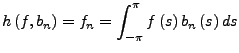
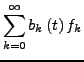
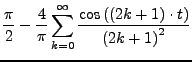
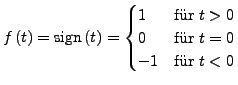
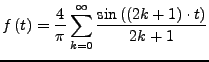
Ist
![]() Lipschitzstetig
(insbesondere
Lipschitzstetig
(insbesondere ![]() -Funktion), so konvergiert die Fourierreihe
punktweise gegen
-Funktion), so konvergiert die Fourierreihe
punktweise gegen ![]() .
.
Ist ![]() sogar
sogar ![]() -Funktion, dann konvergiert die Fourrierreihe
gleichmässig gegen
-Funktion, dann konvergiert die Fourrierreihe
gleichmässig gegen ![]() .
.