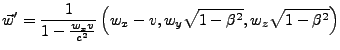Sei das Inertialsystem ![]() gegenüber dem Inertialsystem
gegenüber dem Inertialsystem ![]() entlang
der
entlang
der ![]() -Achse mit der Geschwindigkeit
-Achse mit der Geschwindigkeit ![]() bewegt.
bewegt.
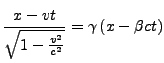 |
|||
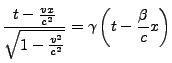 |
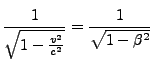 |
|||
Sei das Inertialsystem ![]() gegenüber dem Inertialsystem
gegenüber dem Inertialsystem ![]() entlang
der Geschwindigkeit
entlang
der Geschwindigkeit ![]() (gemessen im System
(gemessen im System ![]() ) bewegt.
) bewegt.
Hierfür werden die Formeln aus der Speziellen Lorentztransformation
genutzt, allerdings der Vektor
![]() wird
in zwei Komponenten zerlegt
wird
in zwei Komponenten zerlegt
Dabei ist
![]() die Komponente von
die Komponente von ![]() in Richtung
in Richtung
![]() , und
, und
![]() die senkrecht dazu. Nun könnte
man einfach
die senkrecht dazu. Nun könnte
man einfach
![]() wie in der speziellen Lorenztransformation
verändern, und
wie in der speziellen Lorenztransformation
verändern, und
![]() gleich belassen unter der Transformation.
Dies eingesetzt ergibt:
gleich belassen unter der Transformation.
Dies eingesetzt ergibt:
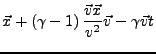 |
|||
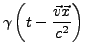 |
Sei ![]() relativ zu
relativ zu ![]() entlang der
entlang der ![]() -Achse mit
-Achse mit
![]() bewegt. Eine Geschwindigkeit
bewegt. Eine Geschwindigkeit
![]() im System
im System ![]() sieht aus dem System
sieht aus dem System ![]() betrachtet wie folgt aus
betrachtet wie folgt aus