Lineare Gleichungssysteme und Matrizen

Definition

Betrachte das LGS über dem Körper $K$ aus Abschnitt sub:LGS. Wir fassen die Koeffizienten $a_{ij}$ in der Matrix

$$A=\left(\begin{array}{ccc} a_{11} & \ldots & a_{1n}\\ \vdots & \ddots & \vdots\\ a_{m1} & \ldots & a_{mn}\end{array}\right)\in K^{m\times n}$$

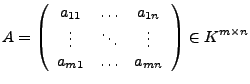
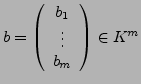zusammen. Ähnlich $b=\left(\begin{array}{c} b_{1}\\ \vdots\\ b_{m}\end{array}\right)\in K^{m}$. Wenn wir die Unbestimmten zu einem Vektor 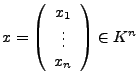$x=\left(\begin{array}{c} x_{1}\\ \vdots\\ x_{n}\end{array}\right)\in K^{n}$ formal zusammenfassen, dann lässt sich das LGS aus sub:LGS schreiben als

$$Ax=b$$

Das zugehörige homogene LGS ist dann

$$Ax=0$$

Lösungen eines homogenen Systems

Die Lösungen von $Ax=0$ bilden einen Unterraum $U\le K^{n}$. Dabei ist

$$\dim U=\textrm{dim}\left(\textrm{ker}A\right)=n-\textrm{rank}A:=k$$

Eine Basis $\left(u_{1},\ldots,u_{k}\right)$ von $U$ heißt System von Fundamentallösungen von $Ax=0$. Jede Lösung von $Ax=0$ ist Linearkombination von den Fundamentallösungen $u_{1},\ldots,u_{k}$.

Existenz von Lösungen

• Das homogene System $Ax=0$ hat stets die (trivial) Lösung $x=0\in K^{n}$.
• Das inhomogene System $Ax=b$ hat genau dann (mindestens) eine Lösung, wenn $b\in$ Spaltenraum von A, bzw. $\textrm{rank}\left(A\vert b\right)=\textrm{rank}\left(A\right)$.

Wobei

$$\left(A\vert b\right)=\left(\begin{array}{cccc} a_{11} & \ldots &... ...{m1} & \ldots & a_{mn} & b_{m}\end{array}\right)\in K^{m\times\left(n+1\right)}$$

Lösungen eines inhomogenen Systems

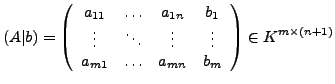
Angenommen das inhomogene System $Ax=b$ hat Lösung $x_{0}\in K^{n}$. Dann ist

$$x_{0}+U=\left\{ x_{0}+x\vert x\in U\right\}$$

die Menge aller Lösungen von $Ax=b$.

eindeutige Lösbarkeit

Siehe sub:Eigenschaften-invertierbarer-Matrizen.