Permutationen

Definition

Sei $A=\left\{ 1,\ldots,n\right\}$ eine endliche Menge. Eine bijektive Abbildung $\sigma:A\rightarrow A$ wird als Permutation bezeichnet. Die Menge aller Permutation auf einer Menge mit $n$ Elementen mird mit $S_{n}$ abgekürzt.

Eine Permutation wird wie folgt notiert

$$\sigma=\left(\begin{array}{cccc} 1 & 2 & \ldots & n\\ \sigma\lef... ...right) & \sigma\left(2\right) & \ldots & \sigma\left(n\right)\end{array}\right)$$

• $\left\vert S_{n}\right\vert=n!$

Zyklus

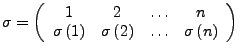
Gilt für eine Permutation $a_{1}\mapsto a_{2},a_{2}\mapsto a_{3},\ldots,a_{k}\mapsto a_{1}$ mit paarweise verschiedenen $a_{i}\in A,\left(i\ge1\right)$, wobei die übrigen Elemente identisch abgebildet werden, so heißt sie eine zyklische Permutation bzw. Zyklus. Ein solches Zykel wird in der Form $\left(a_{1},a_{2},\ldots,a_{k}\right)$ notiert.

• Zwei Zykeln $\pi=\left(a_{1},\ldots,a_{k}\right),\sigma=\left(b_{1},\ldots,b_{l}\right)$ heißen elementfremd, wenn sie disjunhkte Elemente bewegen. d.h. wenn $a_{i}\neq b_{j}$ für alle $j,j$.
• Elementfremde Zykel sind bezüglich kommutativ bezüglich Verkettung.
• Jede Permutation lässt sich als eine verkettung von elementfremden Zykeln schreiben

Transposition

Eine Transposition ist eine Permutation, die nur zwei Elemente vertauscht.

• Jedes Zykel lässt sich mit Hilfe der Verkettung aus Transpositionen darstellen.

Inversion und Signum, gerade und ungerade

Sei $\varphi:\left\{ 1,2,\ldots,n\right\} \rightarrow\left\{ 1,2,\ldots,n\right\}$ eine Permutation. Eine Inversion der Permutation ist ein Paar $\left(i,j\right)$ mit $i<j$ und $\varphi\left(i\right)>\varphi\left(j\right)$. Sei $I\left(\varphi\right)$ die Anzahl der Inversionen von $\varphi$. Wir definieren das Signum $\textrm{sign}:S_{n}\rightarrow\left\{ -1,1\right\}$ durch $\textrm{sign}\left(\sigma\right)=\left(-1\right)^{I\left(\sigma\right)}$ und nennen eine Permutation (un)gerade, wenn wenn sie eine (un)gerade Anzahl von Inversionen hat.

• $\sigma$ ist ungerade $\Leftrightarrow$ $\textrm{sign}\left(\sigma\right)=-1$
• $\sigma$ ist gerade $\Leftrightarrow$ $\textrm{sign}\left(\sigma\right)=1$
• Transpositionen sind ungerade
• Ein Zyklus $\sigma$ mit $k$ Elementen hat $\textrm{sign}\left(\sigma\right)=\left(-1\right)^{k+1}$
• $\textrm{sign}\left(\sigma\circ\pi\right)=\textrm{sign}\left(\sigma\right)\cdot\textrm{sign}\left(\pi\right)$