




Next: Euklidische und unitäre Vektorräume
Up: Determinanten
Previous: Permutationen
Contents
Index
Subsections
Eine Abbildung
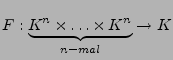 (für
(für 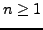 ) heißt:
) heißt:
- Multilinearform auf
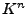
- (oder
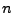 -Form)
falls gilt:
-Form)
falls gilt:
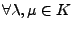
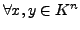
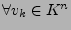
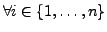
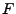 ist linear in jedem Argument
ist linear in jedem Argument
- Addition von Multilinearformen und Multiplikation mit einem Skalar
behalten Multlinearität bei
- alternierende Multilinearform auf
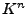
- falls
zusätzlich gilt:
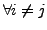
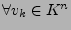
falls
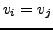 für
für 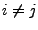
- Hieraus folgt: für
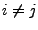
- Falls
 eine alternierende Multilinearform mit
eine alternierende Multilinearform mit
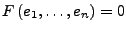 ist, folgt dass
ist, folgt dass 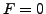 sein muss.
sein muss.
- Wenn
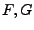 zwei alternierende Multilinearfomens sind, gilt
zwei alternierende Multilinearfomens sind, gilt
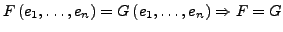
- Determinantenform auf
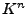
- (auch
normiert alternierende Multilinearform)
fall zusätzlich gilt:
- auf
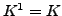 ist die einzige mögliche Determinantenform
ist die einzige mögliche Determinantenform
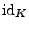
- Die Abbildung
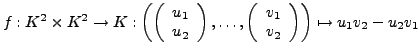 ist Determinantenform auf
ist Determinantenform auf 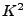
- Die Determinantenform ist so bereits eindeutig definiert
Sei
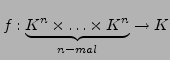 eine Determinantenform und
eine Determinantenform und
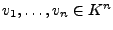 . Falls
. Falls
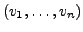 linear abhängig, gilt
linear abhängig, gilt
Laplace Entwicklung
Konstruiere Determinantenform 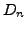 auf
auf 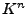 .
.
Für 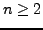 konstruiere induktiv Determinantenform für
konstruiere induktiv Determinantenform für
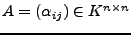 für ein beliebiges
für ein beliebiges
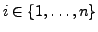 . Dabei ist
. Dabei ist
die Matrix 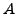 bei der die
bei der die 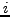 -te Zeile und die
-te Zeile und die 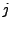 -te Spalte gestrichen
wurden.
-te Spalte gestrichen
wurden.
- Notation: Statt
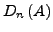 schreibe
schreibe
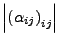
- Diese Formel wird auch die Entwicklung nach einer Spalte genannt
- Alternativ lässt sich auch nach einer Zeile entwickeln
Die Abbildung
heißt die Determinante auf 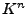 .
.
-
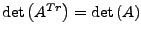
-
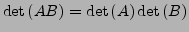
- Falls
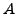 invertierbar, gilt
invertierbar, gilt
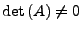 und
und
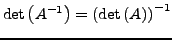
-
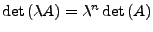
Eigenschaften invertierbarer
Matrizen
Sei
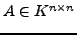 eine quadratische Matrix. Äquivalent sind:
eine quadratische Matrix. Äquivalent sind:
-
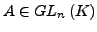 , d.h.
, d.h. 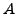 ist invertierbar
ist invertierbar
-
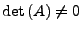
-
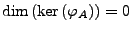
- Das LGS
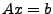 ist für alle
ist für alle
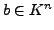 eindeutig lösbar
eindeutig lösbar
- Die Spalten von
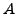 sind linear unabhängig
sind linear unabhängig
- Die Zeilen von
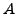 sind linear unabhängig
sind linear unabhängig
-
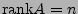
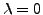 ist kein Eigenwert von
ist kein Eigenwert von 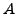
Zwei Matrizen
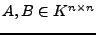 heißen ähnlich,
falls es ein
heißen ähnlich,
falls es ein
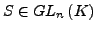 gibt mit
gibt mit
- ähnliche Matrizen haben die gleiche Determinante, gleiche Spur und
gleiches charakterisitsches Polynom
- siehe Basiswechsel sub:Basiswechsel-von-Abbildungen.
Seien
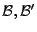 Basen von
Basen von 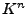 und
und
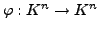 linear. Dann existiert ein
linear. Dann existiert ein
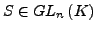 mit
mit
Dies bedeutet, das die die Determinante zu einer linearen Abbildung
unabhängig von der konkreten Wahl der Basis ist.
- Siehe auch sub:Matrix-bez=FCglich-Basen.
Leibnizformel
Sei
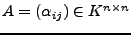 . Es gilt
. Es gilt
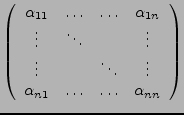
Sei
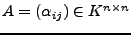 eine obere
Dreiecksmatrix,
d.h.
eine obere
Dreiecksmatrix,
d.h.
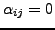 für
für 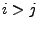 . Dann gilt
. Dann gilt
- gleiches gilt für untere Dreiecksmatrizen,
d.h.
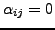 für
für 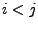
- Entspricht dem Produkt der Diagonalelementen
Sei
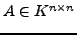 belibig. Der Gauß-Jordan-Eliminationsalgorithmus
(siehe sub:Gauss-Jordan) formt
belibig. Der Gauß-Jordan-Eliminationsalgorithmus
(siehe sub:Gauss-Jordan) formt 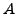 um durch endlich viele
elementare Zeilenoperationen (siehe sub:Zeilenoperationen)
zu einer Matrix
um durch endlich viele
elementare Zeilenoperationen (siehe sub:Zeilenoperationen)
zu einer Matrix 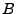 in Zeilenstufenform (insbesondere obere Dreiecksmatrix).
in Zeilenstufenform (insbesondere obere Dreiecksmatrix).
Die elementaren Zeilenumformungen entsprechen einer Multiplikation
mit einer Matrix von Links. Die Determinanten dieser Matrizen müssen
berücksichtigt werden:
-
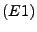
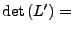 1 (Addition eines vielfachen
einer Zeile zu einer anderen)
1 (Addition eines vielfachen
einer Zeile zu einer anderen)
-
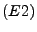
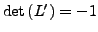 (Vertauschung zweier
Zeilen)
(Vertauschung zweier
Zeilen)
-
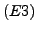
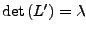 (Multiplikation
einer Zeilen mit
(Multiplikation
einer Zeilen mit 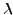 )
)
Falls man sich also bei jeder Umformung diese Konstanten merkt und
aufmultipliziert, kann man sie hinterher wieder herausteilen, und
erhält somit die Determinante von 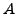 als Produkt der Diagonalen
von
als Produkt der Diagonalen
von 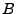 geteilt durch diese Konstanten.
geteilt durch diese Konstanten.
Für eine Blockmatrix
mit
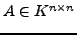 ,
,
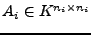 ,
,
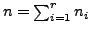 gilt
.
gilt
.
Sei
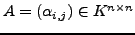 . Mit
. Mit
heißt die Matrix
die Adjungierte oder Adjunkte
von 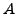 .
.





Next: Euklidische und unitäre Vektorräume
Up: Determinanten
Previous: Permutationen
Contents
Index
Marco Möller 20:09:10 02.12.2005
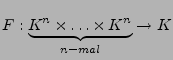 (für
(für 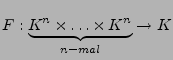 (für
(für ![]() ) heißt:
) heißt:
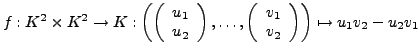 ist Determinantenform auf
ist Determinantenform auf 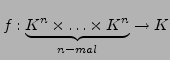 eine Determinantenform und
eine Determinantenform und
![]() . Falls
. Falls
![]() linear abhängig, gilt
linear abhängig, gilt
![]() auf
auf ![]() .
.
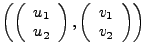
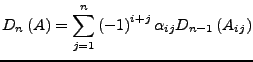

![]() eine quadratische Matrix. Äquivalent sind:
eine quadratische Matrix. Äquivalent sind:
![]() heißen ähnlich,
falls es ein
heißen ähnlich,
falls es ein
![]() gibt mit
gibt mit
![]() Basen von
Basen von ![]() und
und
![]() linear. Dann existiert ein
linear. Dann existiert ein
![]() mit
mit
![]() . Es gilt
. Es gilt

![]() eine obere
Dreiecksmatrix,
d.h.
eine obere
Dreiecksmatrix,
d.h.
![]() für
für ![]() . Dann gilt
. Dann gilt
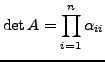
![]() belibig. Der Gauß-Jordan-Eliminationsalgorithmus
(siehe sub:Gauss-Jordan) formt
belibig. Der Gauß-Jordan-Eliminationsalgorithmus
(siehe sub:Gauss-Jordan) formt ![]() um durch endlich viele
elementare Zeilenoperationen (siehe sub:Zeilenoperationen)
zu einer Matrix
um durch endlich viele
elementare Zeilenoperationen (siehe sub:Zeilenoperationen)
zu einer Matrix ![]() in Zeilenstufenform (insbesondere obere Dreiecksmatrix).
in Zeilenstufenform (insbesondere obere Dreiecksmatrix).

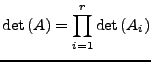
![]() . Mit
. Mit
