




Next: Geometrische Eigenschaften euklidischer und
Up: Euklidische und unitäre Vektorräume
Previous: Hermitesche Skalarprodukt
Contents
Index
Subsections
-
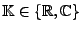
- Für
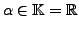 setze
setze
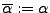
- Hiermit gilt, das Symmetrie ein Spezialfall ist von Hermitsch und
Bilinear ein Spezialfall ist von Semibilinear
Sei 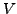 ein
ein
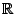 -VR mit einer symmetrischen und positiv
definiten Bilinearform
-VR mit einer symmetrischen und positiv
definiten Bilinearform
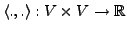 .
Dann heißt
.
Dann heißt
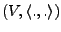 euklidischer
Raum.
euklidischer
Raum.
Sei 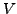 ein
ein
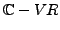 mit einer hermiteschen und positiv definiten
Semibilinearform
mit einer hermiteschen und positiv definiten
Semibilinearform
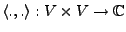 .
Dann heißt
.
Dann heißt
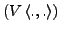 unitärer
Raum.
unitärer
Raum.
Sei
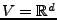 oder
oder
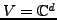 . Außer
. Außer
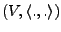 ist
auch jeder Teilraum mit entsprechend eingeschränkten Skalarprodukt
ein euklidischer bzw. unitärer Raum.
ist
auch jeder Teilraum mit entsprechend eingeschränkten Skalarprodukt
ein euklidischer bzw. unitärer Raum.
Sei
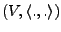 ein unitärere
Raum. Insbesondere ist
ein unitärere
Raum. Insbesondere ist 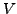 ein
ein
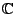 -VR mit Skalarmultiplikation
-VR mit Skalarmultiplikation
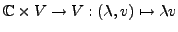 .
Diese lässt sich einschränkend zur Abbildung
.
Diese lässt sich einschränkend zur Abbildung
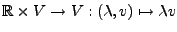 und man erhält einen reellen Vektorraum
und man erhält einen reellen Vektorraum
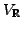 .
Weiter ist dann
.
Weiter ist dann
eine
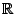 -Bilinearform auf
-Bilinearform auf
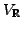 , die symmetrisch
und wiederum positiv definit ist, d.h.
, die symmetrisch
und wiederum positiv definit ist, d.h.
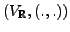 ist ein euklidischer Raum.
ist ein euklidischer Raum.
-
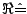 Realteil
Realteil
Sei
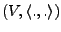 ein euklidischer
oder unitärer Raum. Dann definiert
ein euklidischer
oder unitärer Raum. Dann definiert
die Norm (Länge) von 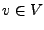 .
Ferner heißen
.
Ferner heißen 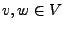 orthogonal (rechtwinklig),
falls
orthogonal (rechtwinklig),
falls
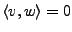 . Schreibe hierfür
. Schreibe hierfür 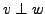 .
Vektoren der Norm
.
Vektoren der Norm 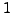 heißen Einheitsvektoren.
heißen Einheitsvektoren.





Next: Geometrische Eigenschaften euklidischer und
Up: Euklidische und unitäre Vektorräume
Previous: Hermitesche Skalarprodukt
Contents
Index
Marco Möller 20:09:10 02.12.2005
![]() ein
ein
![]() -VR mit einer symmetrischen und positiv
definiten Bilinearform
-VR mit einer symmetrischen und positiv
definiten Bilinearform
![]() .
Dann heißt
.
Dann heißt
![]() euklidischer
Raum.
euklidischer
Raum.
![]() ein
ein
![]() mit einer hermiteschen und positiv definiten
Semibilinearform
mit einer hermiteschen und positiv definiten
Semibilinearform
![]() .
Dann heißt
.
Dann heißt
![]() unitärer
Raum.
unitärer
Raum.
![]() oder
oder
![]() . Außer
. Außer
![]() ist
auch jeder Teilraum mit entsprechend eingeschränkten Skalarprodukt
ein euklidischer bzw. unitärer Raum.
ist
auch jeder Teilraum mit entsprechend eingeschränkten Skalarprodukt
ein euklidischer bzw. unitärer Raum.
![]() ein unitärere
Raum. Insbesondere ist
ein unitärere
Raum. Insbesondere ist ![]() ein
ein
![]() -VR mit Skalarmultiplikation
-VR mit Skalarmultiplikation
![]() .
Diese lässt sich einschränkend zur Abbildung
.
Diese lässt sich einschränkend zur Abbildung
![]() und man erhält einen reellen Vektorraum
und man erhält einen reellen Vektorraum
![]() .
Weiter ist dann
.
Weiter ist dann
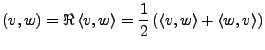
![]() ein euklidischer
oder unitärer Raum. Dann definiert
ein euklidischer
oder unitärer Raum. Dann definiert