Next: Orthonormalbasen
Up: Euklidische und unitäre Vektorräume
Previous: Geometrische Eigenschaften euklidischer und
Contents
Index
Subsections
Seine Menge 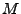 mit einer Abbildung
mit einer Abbildung
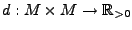 ,
der Metrik, heißt metrischer Raum,
falls
,
der Metrik, heißt metrischer Raum,
falls
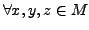
-
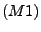
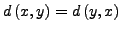
-
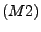
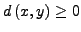 und
und
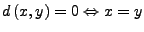
-
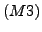
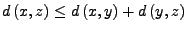
Dreiecksungleichung
Sei
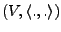 ein euklidischer
oder unitärer Raum. Dann definiert
ein euklidischer
oder unitärer Raum. Dann definiert
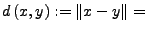
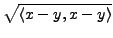 eine Metrik auf
eine Metrik auf 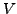 .
.
-
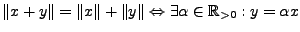
-
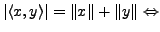
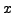 und
und 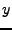 linear abhängig über
linear abhängig über
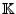
- Existenz genau eines Mittelpunktes auf
der Verbindungsstrecke.
Sei
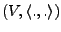 euklidischer Raum.
Dann gilt:
euklidischer Raum.
Dann gilt:
- Sei
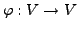 eine Abbildung mit
eine Abbildung mit
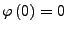 und
und
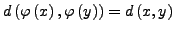 für alle
für alle 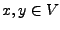 .
. 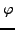 ist linear.
ist linear.
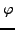 nennt sich abstandserhaltend
oder isometrie
nennt sich abstandserhaltend
oder isometrie
- siehe sub:Orthogonale-und-unitaere Abb





Next: Orthonormalbasen
Up: Euklidische und unitäre Vektorräume
Previous: Geometrische Eigenschaften euklidischer und
Contents
Index
Marco Möller 20:09:10 02.12.2005
![]() mit einer Abbildung
mit einer Abbildung
![]() ,
der Metrik, heißt metrischer Raum,
falls
,
der Metrik, heißt metrischer Raum,
falls
![]()
![]() ein euklidischer
oder unitärer Raum. Dann definiert
ein euklidischer
oder unitärer Raum. Dann definiert
![]()
![]() eine Metrik auf
eine Metrik auf ![]() .
.