




Next: Eigenwerte und Eigenvektoren
Up: Euklidische und unitäre Vektorräume
Previous: Fourierreihe
Contents
Index
Subsections
Orthogonale und unitäre
Abbildungen
Sei
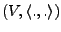 ein euklidischer
oder unitärer Raum.
ein euklidischer
oder unitärer Raum.
Eine invertierbare Abbildung
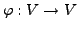 heißt orthogonal
(bzw. unitär), falls gilt
heißt orthogonal
(bzw. unitär), falls gilt
nennt sich 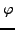 eine Isometrie.
eine Isometrie.
- Orthogonale (und unitäre) Abbildungen respektieren Längen und Winkel
- Für
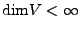 folgt die Invertierbarkeit aus der Isometrieeigenschaft.
folgt die Invertierbarkeit aus der Isometrieeigenschaft.
Es seien 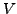 und
und 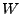 zwei euklidische oder unitäre Vektorräume und
es sei
zwei euklidische oder unitäre Vektorräume und
es sei
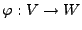 eine lineare Abbildung. Folgende
Aussagen sind äquivalent:
eine lineare Abbildung. Folgende
Aussagen sind äquivalent:
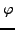 ist eine Isometrie
ist eine Isometrie
-
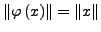 für alle
für alle 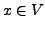
-
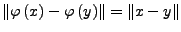 für alle
für alle 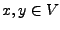
Für
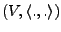 euklidisch heißt
euklidisch heißt
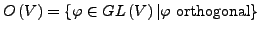 orthogonale Gruppe auf
orthogonale Gruppe auf 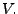 Für
Für
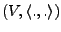 unitär heißt
unitär heißt
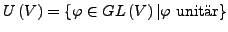 unitäre Gruppe auf
unitäre Gruppe auf 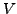 .
.
Sei
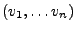 eine Orthonormalbasis von
eine Orthonormalbasis von 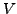 .
Es gilt
.
Es gilt
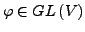 orthogonal bzw. unitär
orthogonal bzw. unitär
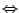
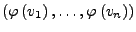 ist Orthonormalbasis.
ist Orthonormalbasis.
- D.h. das die Spalten/Zeilen von
![$ \left[\varphi\right]_{I_{n}}^{I_{n}}$](img846.png) bilden ein Orthonormalsystem
bilden ein Orthonormalsystem
Eine Matrix
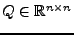 heißt orthogonal,
falls gilt
heißt orthogonal,
falls gilt
-
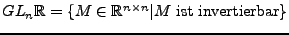
-
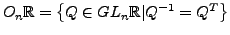 heißt orthogonale Gruppe auf
heißt orthogonale Gruppe auf
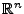 .
.
-
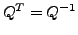
-
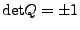
Für
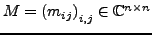 heißt
heißt
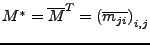 die
zu
die
zu 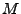 adjungierte Matrix.
adjungierte Matrix.
Eine Matrix
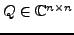 heißt unitär,
falls
heißt unitär,
falls
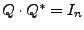 .
.
-
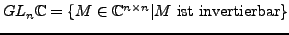
-
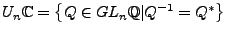 heißt unitäre Gruppe auf
heißt unitäre Gruppe auf
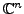 .
.
- Menge der invertierbaren Matritzen
- So etwas wie Drehungen und Spiegelungen in komplexen Vektorräumen
- Drehungen und Spiegelungen in reellen Vektorräumen
- beschreiben Drehungen in reellen Vektorräumen
- Alle hier aufgelisteten Gruppen sind Untergruppen von
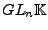 .
D.h. die Elemente sind eine Teilmenge (
.
D.h. die Elemente sind eine Teilmenge (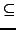 ), und sie sind
unter der Verknüpfung abgeschlossen. Hierzu nutze wie beim Untervektorraum
das Symbol
), und sie sind
unter der Verknüpfung abgeschlossen. Hierzu nutze wie beim Untervektorraum
das Symbol 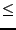 .
.
- Verkettung von Drehungen ist Drehung
- Verkettung von Drehung und Spiegelung ist Spiegelung
- Verkettung von Spiegelungen ist Drehung
Es sei
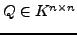 . Äquivalent sind:
. Äquivalent sind:
- Die lineare Abbildung
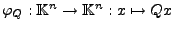 ist orthogonal (bzw. unitär) bzgl. des euklidischen Skalarprodukts
(bzw. bzgl. des hermitschen Skalarprodukts), d.h.
ist orthogonal (bzw. unitär) bzgl. des euklidischen Skalarprodukts
(bzw. bzgl. des hermitschen Skalarprodukts), d.h.
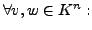
- Die Spalten
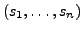 der Matrix
der Matrix 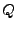 bilden
eine Orthonormalbasis von
bilden
eine Orthonormalbasis von
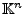 : d.h.
: d.h.
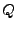 ist eine orthogonale Matrix, d.h.
ist eine orthogonale Matrix, d.h.
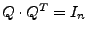 (bzw.
unitär
(bzw.
unitär
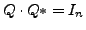 )
)
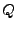 ist invertierbar und
ist invertierbar und
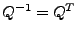 (bzw.
(bzw. 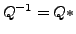 )
)
- Die Zeilen von
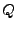 bilden eine Orthonormalbasis)
bilden eine Orthonormalbasis)
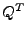 ist eine orthogonale Matrix (bzw. unitär)
ist eine orthogonale Matrix (bzw. unitär)
Es sei 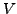 ein euklidischer Vektorraum. Ist
ein euklidischer Vektorraum. Ist 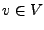 ein Einheitsvektor
(d.h.
ein Einheitsvektor
(d.h.
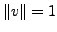 ) so wird durch
) so wird durch
eine Abbildung definiert, die orthogonale Spiegelung
an der zu 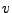 orthogonalen Hyperebene heißt.
orthogonalen Hyperebene heißt.
-
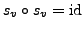
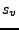 ist linear und orthogonal
ist linear und orthogonal





Next: Eigenwerte und Eigenvektoren
Up: Euklidische und unitäre Vektorräume
Previous: Fourierreihe
Contents
Index
Marco Möller 20:09:10 02.12.2005
![]() ein euklidischer
oder unitärer Raum.
ein euklidischer
oder unitärer Raum.
![]() heißt orthogonal
(bzw. unitär), falls gilt
heißt orthogonal
(bzw. unitär), falls gilt
![]() und
und ![]() zwei euklidische oder unitäre Vektorräume und
es sei
zwei euklidische oder unitäre Vektorräume und
es sei
![]() eine lineare Abbildung. Folgende
Aussagen sind äquivalent:
eine lineare Abbildung. Folgende
Aussagen sind äquivalent:
![]() euklidisch heißt
euklidisch heißt
![]() orthogonale Gruppe auf
orthogonale Gruppe auf ![]() Für
Für
![]() unitär heißt
unitär heißt
![]() unitäre Gruppe auf
unitäre Gruppe auf ![]() .
.
![]() eine Orthonormalbasis von
eine Orthonormalbasis von ![]() .
Es gilt
.
Es gilt
![]() orthogonal bzw. unitär
orthogonal bzw. unitär
![]()
![]() ist Orthonormalbasis.
ist Orthonormalbasis.
![]() heißt orthogonal,
falls gilt
heißt orthogonal,
falls gilt
![]() heißt
heißt
![]() die
zu
die
zu ![]() adjungierte Matrix.
adjungierte Matrix.
![]() heißt unitär,
falls
heißt unitär,
falls
![]() .
.
![]() . Äquivalent sind:
. Äquivalent sind:
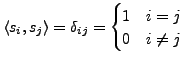
![]() ein euklidischer Vektorraum. Ist
ein euklidischer Vektorraum. Ist ![]() ein Einheitsvektor
(d.h.
ein Einheitsvektor
(d.h.
![]() ) so wird durch
) so wird durch