




Next: Polynome
Up: Eigenwerte und Eigenvektoren
Previous: Einleitung
Contents
Index
Subsections
Seien
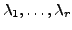 paarweise verschiedene Eigenwerte
von
paarweise verschiedene Eigenwerte
von 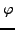 und
und
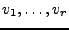 zugehörige Eigenvektoren.
Dann ist
zugehörige Eigenvektoren.
Dann ist
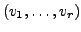 linear unabhängig.
linear unabhängig.
- Falls
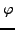 sogar
sogar
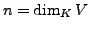 verschiedene Eigenwerte hat,
so ist
verschiedene Eigenwerte hat,
so ist 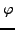 diagonalisierbar.
diagonalisierbar.
Diagonalisierung von Abbildung
Seien
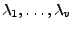 verschiedene Eigenwerte von
verschiedene Eigenwerte von
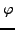 mit den geometrischen Vielfachheiten
mit den geometrischen Vielfachheiten
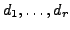 .
Sei
.
Sei
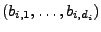 Basis für
Basis für
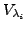 .
Dann ist
.
Dann ist
Basis von
Falls gilt
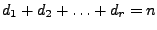 , dann gilt
und
, dann gilt
und 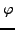 ist diagonalisierbar.
ist diagonalisierbar.
Marco Möller 20:09:10 02.12.2005
![]() paarweise verschiedene Eigenwerte
von
paarweise verschiedene Eigenwerte
von ![]() und
und
![]() zugehörige Eigenvektoren.
Dann ist
zugehörige Eigenvektoren.
Dann ist
![]() linear unabhängig.
linear unabhängig.
![]() verschiedene Eigenwerte von
verschiedene Eigenwerte von
![]() mit den geometrischen Vielfachheiten
mit den geometrischen Vielfachheiten
![]() .
Sei
.
Sei
![]() Basis für
Basis für
![]() .
Dann ist
.
Dann ist
![$\displaystyle \left[\varphi\right]_{B}^{B}=\left(\begin{array}{ccc}
\overbrace{...
...lambda_{r}\\
& \ddots\\
& & \lambda_{r}\end{array}}_{d_{r}}\end{array}\right)$](img921.png)