Polynome

Sei $K$ ein Körper.

Polynom

Eine Funktion $a:\mathbb{N}\rightarrow K:n\mapsto a_{n}$ mit der Eigenschaft, dass es ein $N\in\mathbb{N}$ gibt, so dass $\forall n>N:a_{n}=0$ gilt heißt Polynom mit Koeffizienten in $K$.

Wir schreiben solch eine Funktion $a=\left(a_{0},a_{1},a_{2},\ldots,a_{N},0,\ldots\right)$ als $a\left(t\right)=a_{0}+a_{1}t+a_{2}t^{2}+\ldots+a_{n}t^{N}$, wobei das Symbol $t$ eine Unbestimmte (insbesondere kein Element aus $K$) ist.

$K\left[t\right]=\left\{ a_{0}+a_{1}t+\ldots+a_{N}t^{N}\vert a_{i}\in K,N\in\mathbb{N}\right\}$ ist die Menge aller Polynome mit Koeffizienten in $K$ (in der Unbestimmten $t$).

Operationen mit Polynomen

Mit der Komponentenweise Addition und der Komponentenweise Skalarmultiplikation ist $K\left[t\right]$ ein $K$-VR mit Basis $\left(1,t,t^{2},\ldots\right)$. Insbesondere ist $\dim_{K}K\left[t\right]=\infty$.

Addition

$$\left(a_{0}+a_{1}t+a_{2}t^{2}+\ldots+a_{N}t^{N}\right)$$

$$+\left(b_{0}+b_{1}t+\ldots+b_{M}t^{M}\right)$$

$$= \left(a_{0}+b_{0}\right)+\left(a_{1}+b_{1}\right)t+\ldots$$

$$+\left(a_{\max\left(M,N\right)}+b_{\max\left(M,N\right)}\right)t^{\max\left(M,N\right)}$$

Skalarmultiplikation

$$\lambda\left(a_{0}+a_{1}t+a_{2}t^{2}+\ldots+a_{N}t^{N}\right)$$

$$= \left(\lambda a_{0}\right)+\left(\lambda a_{1}\right)t+\left(\lambda a_{2}\right)t^{2}+\ldots+\left(\lambda a_{N}\right)t^{N}$$

Koordinaten

$$\left(a_{0}+a_{1}t+a_{2}t^{2}+\ldots+a_{N}t^{N}\right)$$

$$= \left(a_{0}\cdot1+a_{1}\cdot t+a_{2}\cdot t^{2}+\ldots+a_{N}\cdot t^{N}\right)$$

Polynommultiplikation

$$\left(a_{0}+a_{1}t+a_{2}t^{2}+\ldots+a_{N}t^{N}\right)*$$

$$\left(b_{0}+b_{1}t+b_{2}t^{2}+\ldots+b_{M}t^{M}\right)$$

$$= \left(a_{0}b_{0}\right)+\left(a_{0}b_{1}+b_{1}a_{0}\right)t+\left(a_{0}b_{2}+a_{1}b_{1}+a_{0}b_{2}\right)t^{2}$$

$$+\ldots+\left(\sum_{i+j=k}a_{i}b_{j}\right)t^{k}+\ldots+a_{N}b_{M}t^{N+M}$$

Struktur von Polynomen

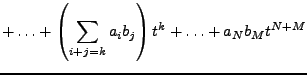$\left(K\left[t\right],+,\cdot,*\right)$ ist eine kommutative $K$-Algebra, das heißt:

1. $\left(K\left[t\right],+,\cdot\right)$ ist ein $K$-Vektorraum
2. $\left(K\left[t\right],+,*\right)$ ist ein kommutativer Ring
3. Es existiert eine Polynommultiplikatives Neutralelement $1=\left(1,0,0,\ldots\right)\in K\left[t\right]$
4. $\left(\lambda\cdot a\right)*b=\lambda\cdot\left(a*b\right)$

Grad

Sei $a:\mathbb{N}\rightarrow K:n\mapsto a_{n}$ ein Polynom. Für $a\neq0$ sei

$$\deg a=\min\left\{ n\in\mathbb{N}\vert\forall n>N:a_{n}=0\right\}$$

und $\deg\left(0\right)=-\infty$. Die Zahl $\deg\left(a\right)\in\mathbb{N}\cup\left\{ -\infty\right\}$ heißt Grad von $a$.

Für alle $n\in\mathbb{N}\cup\left\{ -\infty\right\}$ gilt:

1. $\max\left(n,-\infty\right)=n$
2. $n+\left(-\infty\right)=-\infty$
3. $n\ge-\infty$

Seien $a,b\in K\left[t\right]$, dann gilt:

1. $\deg\left(a+b\right)\le\max\left\{ \deg a,\deg b\right\}$
2. $\deg\left(a\cdot b\right)=\det\left(a\right)+\deg\left(b\right)$

• Für $a,b\in K\left[t\right]\backslash\left\{ 0\right\}$ gilt $a\cdot b=0$, das heißt der Ring ist nullteilerfrei.

Auswertungsabbildung über Körper

Zu einem Polynom $a=a_{0}+a_{1}t+\ldots+a_{N}t^{N}\in K\left[t\right]$ kann man eine Auswertungsabbildung, auch Polynomfunktion genannt, definieren:

$$\tilde{a}:K\rightarrow K:\lambda\mapsto a_{0}+a_{1}\lambda+\ldots+a_{N}\lambda^{N}$$

• kaum Unterschied über Körpern der Charakteristik 0 zu normalem Polynom
• In Fachbüchern wird zwischen dem Polynom und der Auswertungsabbildung meistens nicht unterschieden
• Man kann sich die Auswertungsabbildung von $a\in K\left[t\right]$ in beliebigen $K$-Algebren ansehen
• Ist $K$ unendlich und $p,q\in K\left[t\right]$, so folgt aus $\tilde{p}=\tilde{q}$ schon $p=q$ (umgekehrt ohnehin).

Auswertungsabbildung über Matrizen

Zu einem Polynom $a=a_{0}+a_{1}t+\ldots+a_{N}t^{N}\in K\left[t\right]$ kann man eine Auswertungsabbildung, auch Polynomfunktion genannt, definieren:

$$\tilde{\tilde{a}}:K^{n\times n}\rightarrow K^{n\times n}:M\mapsto a_{0}I_{n}+a_{1}M+\ldots+a_{N}M^{N}$$

• Die Abbildung $\phi_{M}:K\left[t\right]\rightarrow K^{n\times n}:a\mapsto\tilde{\tilde{a}}\left(M\right)$ ist ein $K$-Algebrahomomorphismus.
  Hiermit ist nicht das Polynom, sondern die Auswertungsabbildung des Polynoms gemeint.
• Man kann ebenso eine Auswertungsabbildung in $End_{K}V$ betrachten für beliebigen $K$-Vektorraum $V$
• Der Ring $K\left[t\right]$ ist nullteilerfrei, aber der Ring $K^{n\times n}$ nicht (für $n\ge2$)
• Es gilt für alle $\lambda\in K$
  $\tilde{\tilde{a}}\left(\lambda I_{n}\right)=\tilde{a}\left(\lambda\right)I_{n}$
  das heißt falls $\lambda_{0}$ eine Nullstelle von $a$ ist folgt $\tilde{\tilde{a}}\left(\lambda_{0}I_{n}\right)=0$

Nullstelle

Sei $a\in K\left[t\right]$ ein Polynom. Die Zahl $\lambda\in K$ heißt Nullstelle von $a\in K\left[t\right]$, falls $\tilde{a}\left(\lambda\right)=0$.

Hat $a$ den Grad $d\ge1$ und eine Nullstelle $\lambda\in K$. Dann existiert ein eindeutig bestimmtes Polynom $b\in K\left[t\right]$ mit $\deg b=d-1$ und $a=\left(t-\lambda\right)\cdot b$.

$\left(t-\lambda\right)$ wird Linearfaktor genannt, und das zeilegen von $a$ wird abspalten eines Linearfaktors bezeichnet.

• Die Umkehrung gilt ebenfalls. Falls $a=\left(t-\lambda\right)\cdot b$, dann ist $\lambda$ Nullstelle von $a$.
• Ein Polynom in $K\left[t\right]$ vom Grad $d$ hat höchstens $d$ paarweise verschiedene Nullstellen.

Vielfachheit

Seien $a\in K\left[t\right]$ und $\lambda\in K$, so dass $A=\left(t-\lambda\right)^{s}b$ für $s\in\mathbb{N}\backslash\left\{ 0\right\}$ und $b\in K\left[t\right]$ mit $\tilde{b}\left(\lambda\right)=0$. Dann heißt $s$ die Vielfachheit der Nullstelle $\lambda$ von $a$ und $\lambda$ heißt $s$-fache Nullstelle von $a$.

Seien $\lambda_{1},\ldots,\lambda_{r}$ die verschiedenen Nullstellen von $a\in K\left[t\right]\backslash\left\{ 0\right\}$mit Vielfachheiten $s_{1},\ldots,s_{r}$. Dann existiert eindeutig ein Polynom $b\in K\left[t\right]$ ohne Nullstellen, so dass

$$a=\left(t-\lambda_{1}\right)^{s_{1}}\cdot\ldots\cdot\left(t-\lambda_{r}\right)^{s_{r}}\cdot b$$

Fundamentalsatz der Algebra

Jedes Polynom $a\in\mathbb{C}\left[t\right]$ mit $\deg\ge1$ besitzt eine Nullstelle in $\mathbb{C}$. Das heißt der Körper $\mathbb{C}$ ist algebraisch abgeschlossen. Daraus folgt, dass jedes Polynom in Linearfaktoren und eine Konstante faktorisiert werden kann.

• In den reellen Zahlen kann man faktorisieren in lineare und quadratische Polynome.

Polynomdivision

Sind $p,q\in K\left[t\right]$ mit $q\neq0$, so existieren eindeutig bestimmte Polynome $s,r\in K\left[t\right]$ mit

$$p=s\cdot q+r$$

und $\textrm{deg}\left(r\right)<\textrm{deg}\left(q\right)$. $r$ ist dabei der Rest, ist $r=0$ so sagt man, $p$ ist durch $q$ teilbar.

• Ist $a$ eine Nullstelle des Polynoms $f\in K\left[t\right]$, so ist $f$ durch $\left(x-a\right)$ teilbar.