




Next: Diagonalisierung normaler Matrizen
Up: Eigenwerte und Eigenvektoren
Previous: Polynome
Contents
Index
Subsections
Sei
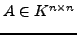 eine quadratische Matrix.
eine quadratische Matrix.
Die Determinante
heißt charakteristisches Polynom
von 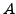 .
.
- Eigentlich sind Polynome eine Körper und somit wäre die Determinante
nicht definiert. Da sich die Polynome
![$ K\left[t\right]$](img930.png) aber in den
Körper der rationalen Funktionen
aber in den
Körper der rationalen Funktionen
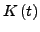 einbetten lassen,
ist dies kein Problem.
einbetten lassen,
ist dies kein Problem.
![$ \chi_{A}\in K\left[t\right]$](img999.png) ist ein Polynom vom Grad
ist ein Polynom vom Grad 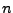 .
.
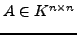 .
Es gilt
.
Es gilt
- Damit lassen sich sich charakteristische Polynome einerseits schnell
überprüfen, und anderseits Polynome vom Grad
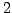 direkt angeben.
direkt angeben.
Die Matrix
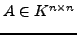 ist diagonalisierbar über
ist diagonalisierbar über 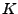 genau
dann, wenn
genau
dann, wenn
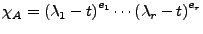 und falls für jeden Eigenwert
und falls für jeden Eigenwert
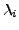 die algebraische
Vielfachheit
die algebraische
Vielfachheit
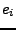 übereinstimmt mit der geometrischen Vielfachheit.
übereinstimmt mit der geometrischen Vielfachheit.
Eine Matrix
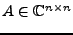 ist diagonalisierbar über
ist diagonalisierbar über
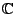 genau dann wenn für jeden Eigenwert stimmen algebraische
und geometrische Vielfachheit überein.
genau dann wenn für jeden Eigenwert stimmen algebraische
und geometrische Vielfachheit überein.
Für
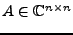 zerfällt
zerfällt 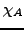 immer in Linearfaktoren.
immer in Linearfaktoren.
Jede komplexe Matrix hat einen Eigenwert.
Sei
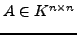 . Dann gilt
. Dann gilt
- Kann benutzt werden um einfache Formeln für höhere Potenzen von Matrizen
zu finden.
Für jede Matrix
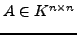 existiert genau ein Polynom
existiert genau ein Polynom
![$ \mu_{A}\in K\left[t\right]$](img1014.png) mit
mit
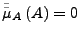 minimalen Grades mit Leitkoeffizienten
minimalen Grades mit Leitkoeffizienten 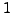 . Der Leitkoeffizient
eines Polynoms
. Der Leitkoeffizient
eines Polynoms
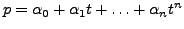 ist für
ist für
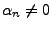 gleich
gleich
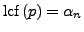 .
.
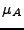 heißt Minimalpolynom von
heißt Minimalpolynom von
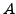 .
.
- Die Existenz annulierender Polynome (Minimalpolynom und Satz von Cayley
Hamilton) ist nur in endlichdimensionalen Vektorräumen gesichert.
- Ähnliche Matrizen haben dasselbe Minimalpolynom
- zu
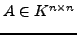 haben
haben 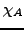 und
und 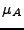 dieselben
Nullstellen
dieselben
Nullstellen
- Das Minimalpolynom teilt das charakteristische Polynom.
- Falls das Charakteristische Polynom keine Nullstelle, bzw. jede nur
mit Algebraischer Vielfachheit
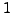 hat gilt:
hat gilt:





Next: Diagonalisierung normaler Matrizen
Up: Eigenwerte und Eigenvektoren
Previous: Polynome
Contents
Index
Marco Möller 20:09:10 02.12.2005
![]() eine quadratische Matrix.
eine quadratische Matrix.
![]() ist ein Polynom vom Grad
ist ein Polynom vom Grad ![]() .
.
![]() .
Es gilt
.
Es gilt
![]() ist diagonalisierbar über
ist diagonalisierbar über ![]() genau
dann, wenn
genau
dann, wenn
![]() und falls für jeden Eigenwert
und falls für jeden Eigenwert
![]() die algebraische
Vielfachheit
die algebraische
Vielfachheit
![]() übereinstimmt mit der geometrischen Vielfachheit.
übereinstimmt mit der geometrischen Vielfachheit.
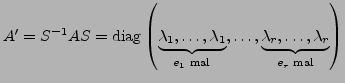 mit
mit
![]() ist diagonalisierbar über
ist diagonalisierbar über
![]() genau dann wenn für jeden Eigenwert stimmen algebraische
und geometrische Vielfachheit überein.
genau dann wenn für jeden Eigenwert stimmen algebraische
und geometrische Vielfachheit überein.
![]() zerfällt
zerfällt ![]() immer in Linearfaktoren.
immer in Linearfaktoren.
![]() . Dann gilt
. Dann gilt
![]() existiert genau ein Polynom
existiert genau ein Polynom
![]() mit
mit
![]() minimalen Grades mit Leitkoeffizienten
minimalen Grades mit Leitkoeffizienten ![]() . Der Leitkoeffizient
eines Polynoms
. Der Leitkoeffizient
eines Polynoms
![]() ist für
ist für
![]() gleich
gleich
![]() .
.
![]() heißt Minimalpolynom von
heißt Minimalpolynom von
![]() .
.