




Next: Vektorräume
Up: Vektroräume
Previous: Vektroräume
Contents
Index
Subsections
Verknüpfungen
- Negation
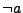 : nicht
: nicht 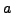
- Implikation
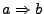 : aus
: aus 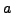 folgt
folgt 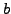
- Äquivalenz
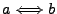 :
: 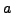 und
und 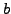 sind äquivalent
(gleichwertig)
sind äquivalent
(gleichwertig)
- Konjunktion
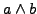 :
: 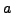 und
und 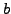
- Disjunktion
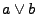 :
: 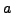 oder
oder 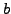
Wahrheitstabelle:
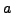 |
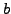 |
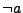 |
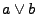 |
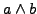 |
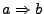 |
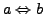 |
| f |
f |
w |
f |
f |
w |
w |
| f |
w |
w |
w |
f |
w |
f |
| w |
f |
f |
w |
f |
f |
f |
| w |
w |
f |
w |
w |
w |
w |
Quantoren
- Allquantor
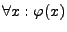
für alle 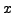 gilt
gilt
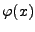 .
.
z.B.
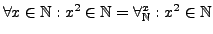
- Existenzquantor
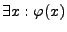
es gibt (mindestens) ein 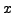 für das
für das
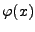 gilt.
gilt.
z.B.
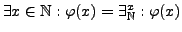
-
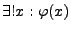 oder
oder
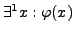
es gibt genau ein 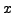 für das
für das
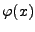 gilt.
gilt.
- Negation
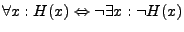
Es gilt für alle 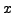 ,
, 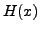
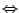 Es gibt nicht ein
Es gibt nicht ein
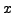 , für das
, für das 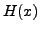 nicht gilt.
nicht gilt.
- Widerspruch
- (Symbol: Blitz) heißt eine zusammengesetzte Aussage,
wenn sie immer falsch ist.
z.B.
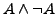
- Tautologie
- heißt eine Aussage, wenn sie immer wahr ist.
z.B.
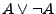
- Potenzmenge
-
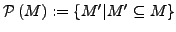
- Differenzmenge
- für
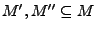 sei
sei

- Menge aller Abbildungen
- Seien
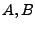 beliebige Mengen. Dann bezeichnet
beliebige Mengen. Dann bezeichnet
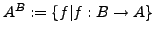 die Menge aller Abbildungen von
die Menge aller Abbildungen von 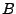 nach
nach 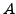 .
.
- Verkettung
- Sei
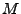 eine beliebige Menge. Die
Verkettung von Abbildungen von
eine beliebige Menge. Die
Verkettung von Abbildungen von 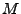 in sich ist definiert durch
in sich ist definiert durch
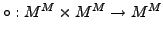 mit
mit
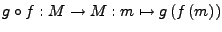 für
für
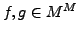 und
und 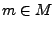 .
.
- Verkettungen sind assoziativ.
- Die Verkettung von bijektiven Abbildungen ist wieder bijektiv
- Sym
-
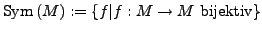
- für
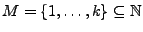 schreibe
schreibe 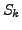 (Menge von allen möglichen Permutationen von
(Menge von allen möglichen Permutationen von 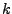 Zahlen)
Zahlen)
Eine (binäre) Verknüpfung 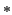 auf einer
Menge
auf einer
Menge 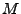 ist eine Abbildung
ist eine Abbildung
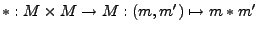 .
Sie heißt
.
Sie heißt
- kommutativ
- falls
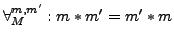
- assoziativ
- falls
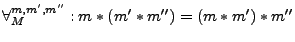
- In diesem Fall ist es nicht nötig Klammern zu setzen.
- Es gibt postfix, infixund
suffix Notationen für Verknüpfungen, jenachdem,
ob das Zeichen vor, zwischen oder nach den Operanden kommt.
- Verknüpfungen sind eine Teilmenge der Abbildungen
Sei 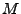 eine beliebige Menge, und
eine beliebige Menge, und 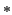 eine assoziative Verknüpfung.
Das Paar
eine assoziative Verknüpfung.
Das Paar
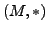 wird nun als Halbgruppe
bezeichnet.
wird nun als Halbgruppe
bezeichnet.
-
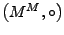 ist eine Halbgruppe
ist eine Halbgruppe
- Eine Halbgruppe mit neutralem Element nennt sich auch ein Monoid.
Eine Halbgruppe
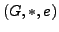 heißt Gruppe,
falls folgene Elemente exisiteren
heißt Gruppe,
falls folgene Elemente exisiteren
- Neutralelement
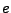
- Inverses Element
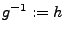
Man sprich von einer kommutativen Gruppe,
falls 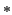 zusätzlich noch kommutativ ist.
zusätzlich noch kommutativ ist.
- jede Gruppe besitzt genau ein neutrales Element
- in einer Gruppe existiert zu jedem Element genau ein inverses
Element
- Eine Gruppe ohne Inverse Elemente nennt sich Monoid
- Falls
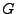 endlich, darf in der Verknüpfungstafel von
endlich, darf in der Verknüpfungstafel von 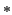 in jeder
Zeile und in jeder Spalte jedes Element nur genau einmal vorkommen.
in jeder
Zeile und in jeder Spalte jedes Element nur genau einmal vorkommen.
- Die Gruppe
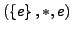 wird als triviale
Gruppe bezeichnet
wird als triviale
Gruppe bezeichnet
-
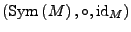 ist
eine Gruppe mit Neutralelement
ist
eine Gruppe mit Neutralelement
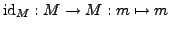
-
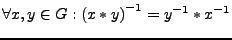
Sei 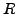 eine Menge mit zwei Verknüpfungen
eine Menge mit zwei Verknüpfungen
 und
und
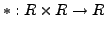 .
. 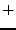 wird mit plus, und
wird mit plus, und 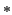 mit
mal bezeichnet. Das Tripel
mit
mal bezeichnet. Das Tripel
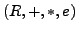 heißt Ring,
falls
heißt Ring,
falls
-
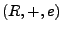 eine kommutative Gruppe ist
eine kommutative Gruppe ist
-
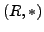 eine Halbgruppe ist
eine Halbgruppe ist
- Es gelten die Distributivgesetze für alle
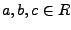
Einen Ring 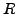 nennt man Ring mit
nennt man Ring mit 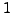 ,
wenn er ein neutrales Element bzgl. der Multiplikation hat, welches
man mit
,
wenn er ein neutrales Element bzgl. der Multiplikation hat, welches
man mit 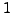 bezeichnet. Man nennt ein
bezeichnet. Man nennt ein 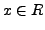 invertierbar,
wenn es ein
invertierbar,
wenn es ein
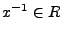 gibt, mit
gibt, mit
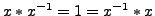 .
.
- In jedem Ring mit
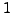 bildet die Menge der invertierbaren Elemente
eine Gruppe.
bildet die Menge der invertierbaren Elemente
eine Gruppe.
- Wenn für
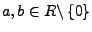
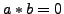 gilt, heißt
der Ring nullteilerfrei. In nullteilerfreien
Ringen kann man eine Division mit Rest
definieren.
gilt, heißt
der Ring nullteilerfrei. In nullteilerfreien
Ringen kann man eine Division mit Rest
definieren.
- In einem Ring mit
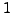 ist jedes Element
ist jedes Element 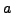 entweder invertierbar
oder Nullteiler (d.h.
entweder invertierbar
oder Nullteiler (d.h.
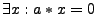 )
)
Ein Ring
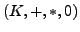 mit additivem (
mit additivem (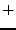 ) Neutralelement
) Neutralelement
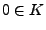 heißt Körper
heißt Körper
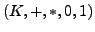 ,
falls zusätzlich
,
falls zusätzlich
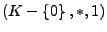 eine kommutative
Gruppe ist. Das additive (
eine kommutative
Gruppe ist. Das additive (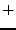 ) Neutralelement 0 heißt Nullelement,
und das multiplikative (
) Neutralelement 0 heißt Nullelement,
und das multiplikative (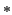 ) Neutralelement heißt Einselement.
) Neutralelement heißt Einselement.
- falls
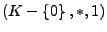 eine nicht kommutative
Gruppe ist, wird
eine nicht kommutative
Gruppe ist, wird
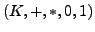 als Schiefkörper
bezeichnet.
als Schiefkörper
bezeichnet.
-
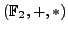 mit und ist der kleinste mögliche Körper.
mit und ist der kleinste mögliche Körper.
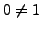 muss gelten
muss gelten
- Körper sind per Nullteilerfrei, d.h. es gilt:

Sei
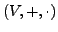 ein
ein 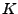 -Vektorraum und
-Vektorraum und
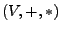 ein Ring mit
ein Ring mit 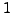 . Dann wird
. Dann wird
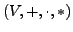 als
als 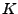 -Algebra
bezeichnet, falls
-Algebra
bezeichnet, falls
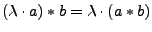 für belibige
für belibige
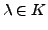 und
und 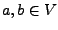 gilt.
gilt.
Eine (zweistellige) Relation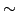 zwischen den
Mengen A und B ist eine Teilmenge von
zwischen den
Mengen A und B ist eine Teilmenge von 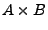 .
.
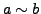 falls
falls
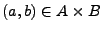 .
.
Wir nennen 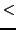 Ordnung oder Anordnung
falls entweder
Ordnung oder Anordnung
falls entweder 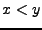 oder
oder 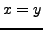 oder
oder 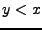 gilt (nur eines dieser
3). Zudem muss
gilt (nur eines dieser
3). Zudem muss 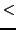 transitiv sein.
transitiv sein.
Ein Ring oder ein Körper
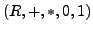 heißt angeordneter
Ring bzw. angeordneter
Körper, schreibe
heißt angeordneter
Ring bzw. angeordneter
Körper, schreibe
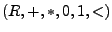 , falls
, falls 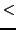 eine Ordnung auf
eine Ordnung auf 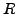 ist
und folgendes für alle
ist
und folgendes für alle
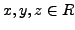 gilt:
gilt:
-
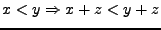
-
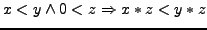
- positiv
- falls
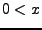
- negativ
- falls
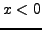
- nicht positiv
- falls
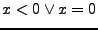
- nicht negativ
- falls
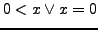
- positiv
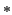 positiv = positiv = negativ
positiv = positiv = negativ 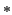 negativ
negativ
- negativ
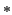 positiv = negativ = positiv
positiv = negativ = positiv 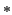 negativ
negativ
-
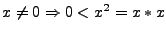
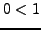
- ein angeordneter Ring / Körper hat unendlich viele Elemente
- es gelte die Punkt vor Strich-Rechnung, um Klammern zu sparen





Next: Vektorräume
Up: Vektroräume
Previous: Vektroräume
Contents
Index
Marco Möller 20:09:10 02.12.2005
![]() auf einer
Menge
auf einer
Menge ![]() ist eine Abbildung
ist eine Abbildung
![]() .
Sie heißt
.
Sie heißt
![]() eine beliebige Menge, und
eine beliebige Menge, und ![]() eine assoziative Verknüpfung.
Das Paar
eine assoziative Verknüpfung.
Das Paar
![]() wird nun als Halbgruppe
bezeichnet.
wird nun als Halbgruppe
bezeichnet.
![]() heißt Gruppe,
falls folgene Elemente exisiteren
heißt Gruppe,
falls folgene Elemente exisiteren
![]() eine Menge mit zwei Verknüpfungen
eine Menge mit zwei Verknüpfungen
![]() und
und
![]() .
. ![]() wird mit plus, und
wird mit plus, und ![]() mit
mal bezeichnet. Das Tripel
mit
mal bezeichnet. Das Tripel
![]() heißt Ring,
falls
heißt Ring,
falls
![]() mit additivem (
mit additivem (![]() ) Neutralelement
) Neutralelement
![]() heißt Körper
heißt Körper
![]() ,
falls zusätzlich
,
falls zusätzlich
![]() eine kommutative
Gruppe ist. Das additive (
eine kommutative
Gruppe ist. Das additive (![]() ) Neutralelement 0 heißt Nullelement,
und das multiplikative (
) Neutralelement 0 heißt Nullelement,
und das multiplikative (![]() ) Neutralelement heißt Einselement.
) Neutralelement heißt Einselement.
![]() ein
ein ![]() -Vektorraum und
-Vektorraum und
![]() ein Ring mit
ein Ring mit ![]() . Dann wird
. Dann wird
![]() als
als ![]() -Algebra
bezeichnet, falls
-Algebra
bezeichnet, falls
![]() für belibige
für belibige
![]() und
und ![]() gilt.
gilt.
![]() zwischen den
Mengen A und B ist eine Teilmenge von
zwischen den
Mengen A und B ist eine Teilmenge von ![]() .
.
![]() falls
falls
![]() .
.
![]() Ordnung oder Anordnung
falls entweder
Ordnung oder Anordnung
falls entweder ![]() oder
oder ![]() oder
oder ![]() gilt (nur eines dieser
3). Zudem muss
gilt (nur eines dieser
3). Zudem muss ![]() transitiv sein.
transitiv sein.
![]() heißt angeordneter
Ring bzw. angeordneter
Körper, schreibe
heißt angeordneter
Ring bzw. angeordneter
Körper, schreibe
![]() , falls
, falls ![]() eine Ordnung auf
eine Ordnung auf ![]() ist
und folgendes für alle
ist
und folgendes für alle
![]() gilt:
gilt: