Eine Matrix
![]() besitzt Jordansche Normalform
falls sie eine Blockdiagonalmatrix aus Jordanblöcken ist, d.h.
besitzt Jordansche Normalform
falls sie eine Blockdiagonalmatrix aus Jordanblöcken ist, d.h.
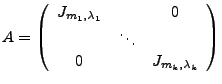
Sei
![]() und
und
![]() . Dann
existiert eine Basis
. Dann
existiert eine Basis
![]() von
von ![]() , so dass
, so dass
![]() Jordansche Normalform hat.
Jordansche Normalform hat.
Sei
![]() . Dann ist
. Dann ist ![]() ähnlich zu einer
Matrix in Jordanscher Normalform.
ähnlich zu einer
Matrix in Jordanscher Normalform.
Zwei komplexe Matrizen sind ähnlich genau dann, wenn sie (bis auf Umordnung der Jordanblöcke) dieselbe Jordansche Normalform haben.