Next: Quadratische Formen
Up: Jordansche Normalform
Previous: verallgemeinerter Eigenvektor
Contents
Index
Sei
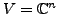 und
und
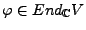 .
.
- Bestimme die Eigenwerte von
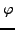 mit algebraischen Vielfachheiten
in
mit algebraischen Vielfachheiten
in
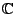 gilt bekanntlich
gilt bekanntlich
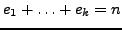 .
.
- Für jeden Eigenwert
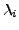 :
:
Bestimme ein Basis des verallgemeinerten Eigenraumes
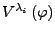 .
Dazu:
.
Dazu:
- schrittweise Lösen der linearen Gleichungssysteme
für
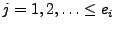 bis man
bis man 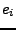 linear unabhängige Lösungen
gefunden hat. Hierbei tauchen die die Lösungen für
linear unabhängige Lösungen
gefunden hat. Hierbei tauchen die die Lösungen für
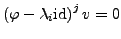 bei
bei
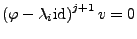 wieder
auf.
wieder
auf.
- Für jeden dieser
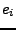 Vektoren
Vektoren 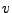 bilde seine Jordanketten durch
anwenden von
bilde seine Jordanketten durch
anwenden von
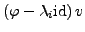 (bis
man 0 erhält).
(bis
man 0 erhält).
- Setze diese Jordanketten zu einer Familie zusammen und verkürze sie
schrittweise durch Anwendung von sub:Jordanfamilie-verkuerzen,
bis man eine Basis (der Länge
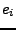 ) erhält.
) erhält.
- Man hat nun also für jedes
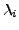 eine Basis der Form
eine Basis der Form
wobei auch die 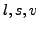 von
von 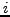 abhängig sind. Es gilt
abhängig sind. Es gilt
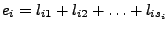 und
und
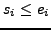
- Matrix des Basiswechsels (zur Jordan Normalform) besitzt als Spalten
verallgemeinerte Eigenvektoren aus 2). Diese Kettenweise aufsteigend
sortieren!
wobei die für die Basiswechselmatrizen gilt





Next: Quadratische Formen
Up: Jordansche Normalform
Previous: verallgemeinerter Eigenvektor
Contents
Index
Marco Möller 20:09:10 02.12.2005
![]() und
und
![]() .
.