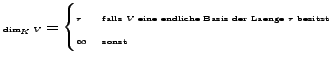Next: Summen in Vektorräumen
Up: Vektroräume
Previous: Gruppen, Ringe, Körper
Contents
Index
Subsections
Sei 
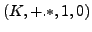 ein Körper. Ein
ein Körper. Ein  -Vektorraum
(Vektorraum über
-Vektorraum
(Vektorraum über  ) ist ein Tripel
) ist ein Tripel
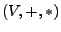 bestehend
aus einer Menge
bestehend
aus einer Menge  , einer binären Verknüpfung
, einer binären Verknüpfung
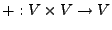 (Addition) und einer Skalarmultiplikation:
(Addition) und einer Skalarmultiplikation:
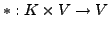 , so dass gilt:
, so dass gilt:
-
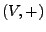 ist eine kommutative Gruppe
ist eine kommutative Gruppe
- für alle
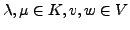 gilt:
gilt:
-
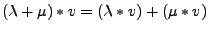
-
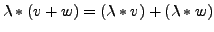
-
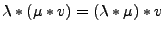
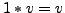
Es gelten folgende Rechenregeln in einem  -VR (Vektorraum)
-VR (Vektorraum)
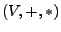 , für alle
, für alle 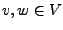 und
und
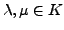 :
:
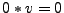
-
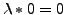
-
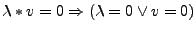
-
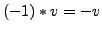
Der Standardvektorraum 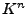 für
für
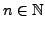 ist wie folgt definiert:
ist wie folgt definiert:
-
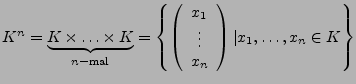
-
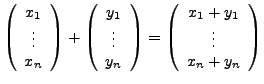
-
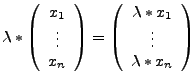
- Nullvektor
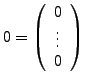 ist das Neutralelement in
ist das Neutralelement in 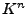
- Die Standardbasisvektoren des
Standardvektorraumes
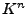 sind
sind
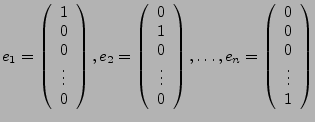
Sei  eine beliebige Menge und
eine beliebige Menge und  ein beliebiger Körper. Es ist
ein beliebiger Körper. Es ist
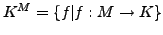 . Mit punktweise
definierter Addition
. Mit punktweise
definierter Addition
und der Skalarmultiplikation
ist
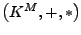 ein
ein  -Vektorraum.
-Vektorraum.
- ist Verallgemeinerung vom Standardvektorraum
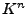 . Hier kann eine
beliebige Menge
. Hier kann eine
beliebige Menge 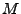 als Index der ``einzelnen Elemente des Vektors''
dienen. Hierfür wäre
als Index der ``einzelnen Elemente des Vektors''
dienen. Hierfür wäre
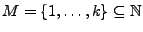
Es sei
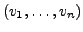 ein geordnetes
ein geordnetes 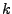 -Tupel
von Vektoren aus einem
-Tupel
von Vektoren aus einem  -VR
-VR  . Ein Vektor
. Ein Vektor 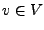 heißt:
heißt:
- Linearkombination
- von
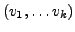 ,
falls
,
falls
- Affinkombination
- von
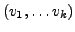 ,
falls
,
falls
- Einschränkung von Linearkombination
- Erzeugen den kleinsten (geringste Anzahl möglicher Vektoren) affinen
Teilraum, der
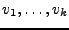 enthält
enthält
- Konvexkombination
- von
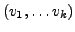 ,
falls
,
falls
- Einschränkung von Affin- und Linearkombination
 muss hierfür ein angeordneter Körper sein.
muss hierfür ein angeordneter Körper sein.
Das (endliche) 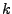 -Tupel
-Tupel
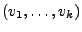 heißt
linear unabhängig, falls
heißt
linear unabhängig, falls
andernfalls heißt
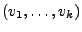 linear
abhängig.
linear
abhängig.
Eine unendliche Familie (Tupel) von Vektoren heißt linear unabhängig,
falls jede endliche Teilfamilie linear unabhängig ist.
Sei  ein VR. Eine nichtleere Teilmenge
ein VR. Eine nichtleere Teilmenge
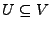 heißt Teilraum
(oder Unterraum) von
heißt Teilraum
(oder Unterraum) von  , falls gilt:
, falls gilt:
Sei  ein
ein  -Vektorraum,
-Vektorraum, 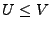 ,
, 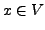 . Dann heißt die
Menge
. Dann heißt die
Menge
affiner Unterraum von 
- Die Lösungen eines inhomogenen LGS sind ein affiner Unterraum
Sei  ein
ein  -Vektorraum und
-Vektorraum und
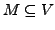 . Die Menge
. Die Menge
heißt lineare Hülle (oder
linearer Aufspann)
von 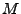 in
in  . Für
. Für
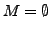 setze
setze
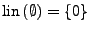 .
.
Sei 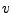 ein
ein  -Vektorraum. Eine Menge
-Vektorraum. Eine Menge
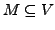 heißt Erzeugendensystem
von
heißt Erzeugendensystem
von  , falls
, falls
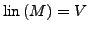 . Eine Familie in V
heißt Basis falls sie ein linear unabhängiges
Erzeugendensystem bildet. Ein Vektorraum heißt endlich erzeugt,
falls er ein endliches Erzeugendensystem besitzt.
. Eine Familie in V
heißt Basis falls sie ein linear unabhängiges
Erzeugendensystem bildet. Ein Vektorraum heißt endlich erzeugt,
falls er ein endliches Erzeugendensystem besitzt.
-
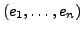 aus
aus 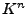 ist eine Basis (Standardbasis)
ist eine Basis (Standardbasis)
Sätze über Basen
Sei
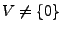 ein
ein  -Vektorraum und sei
-Vektorraum und sei
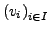 eine Familie von Vektoren aus
eine Familie von Vektoren aus  . Folgende Aussagen sind äquivalent:
. Folgende Aussagen sind äquivalent:
-
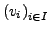 ist eine Basis von
ist eine Basis von 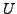
-
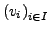 ist ein unverkürzbares
Erzeugendensystem von
ist ein unverkürzbares
Erzeugendensystem von  , d.h.
, d.h.
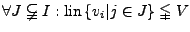
-
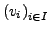 ist ein unverlängerbare
linear unabhängige Familie. D.h.
ist ein unverlängerbare
linear unabhängige Familie. D.h.
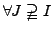 ist
jede Familie von Vektoren
ist
jede Familie von Vektoren
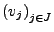 linear abhängig
linear abhängig
- Jeder Vektor aus
 lässt sich eindeutig als Linearkombination
von Vektoren aus
lässt sich eindeutig als Linearkombination
von Vektoren aus
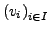 schreiben.
schreiben.
- In jedem endlichen Erzeugendensystem lässt sich eine Teilmenge finden,
die genau eine Basis des Vektorraums ist.
- Jeder Vektorraum hat eine Basis. Bei unendlichen muss dies über das
Auswahlaxiom gezeigt werden.
Basistausch
Austauschlemma: Sei  ein
ein  -Vektorraum
der endlich erzeugt ist. Sei
-Vektorraum
der endlich erzeugt ist. Sei
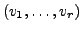 eine
Basis von
eine
Basis von  und sei
und sei
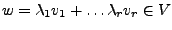 für
für
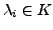 . Dann folgt aus
. Dann folgt aus
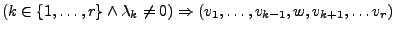 ist eine Basis von
ist eine Basis von  .
.
Austauschsatz: Sei
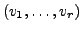 eine Basis der endlich erzeugten Vektroraumes
eine Basis der endlich erzeugten Vektroraumes  , und sei
, und sei
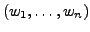 eine linear unabhängige Familie in
eine linear unabhängige Familie in  . Dann gilt
. Dann gilt 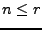 , und
es existieren Indizes
, und
es existieren Indizes
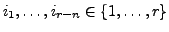 ,
so dass
,
so dass
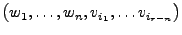 eine Basis von
eine Basis von  sind.
sind.
- Jede Basis eines endlich erzeugten Vektorraumes ist endlich
- Jede Basis von
 hat die selbe Länge (Anzahl in ihr enthaltener
Vektoren)
hat die selbe Länge (Anzahl in ihr enthaltener
Vektoren)
- Jede linear unabhängige Familie in dem endlich erzeugten Vektorraum
 lässt sich zu einer Basis von
lässt sich zu einer Basis von  fortsetzen.
fortsetzen.
Ist  ein
ein  Vektoraum, so heißt
Vektoraum, so heißt
die Dimension von  über K.
über K.
- Sei
 ein
ein  -VR mit
-VR mit
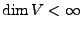 und
und 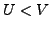 echter Unterraum
von
echter Unterraum
von  . Dann gilt
. Dann gilt
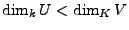 .
.





Next: Summen in Vektorräumen
Up: Vektroräume
Previous: Gruppen, Ringe, Körper
Contents
Index
Marco Möller 20:09:10 02.12.2005
![]()
![]() ein Körper. Ein
ein Körper. Ein ![]() -Vektorraum
(Vektorraum über
-Vektorraum
(Vektorraum über ![]() ) ist ein Tripel
) ist ein Tripel
![]() bestehend
aus einer Menge
bestehend
aus einer Menge ![]() , einer binären Verknüpfung
, einer binären Verknüpfung
![]() (Addition) und einer Skalarmultiplikation:
(Addition) und einer Skalarmultiplikation:
![]() , so dass gilt:
, so dass gilt:
![]() für
für
![]() ist wie folgt definiert:
ist wie folgt definiert:
![]() eine beliebige Menge und
eine beliebige Menge und ![]() ein beliebiger Körper. Es ist
ein beliebiger Körper. Es ist
![]() . Mit punktweise
definierter Addition
. Mit punktweise
definierter Addition
![]() ein geordnetes
ein geordnetes ![]() -Tupel
von Vektoren aus einem
-Tupel
von Vektoren aus einem ![]() -VR
-VR ![]() . Ein Vektor
. Ein Vektor ![]() heißt:
heißt:
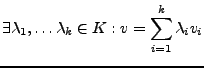
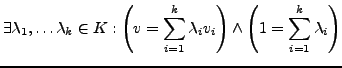
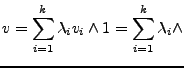
![]() -Tupel
-Tupel
![]() heißt
linear unabhängig, falls
heißt
linear unabhängig, falls
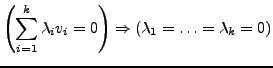
 mit
mit ![]() ein VR. Eine nichtleere Teilmenge
ein VR. Eine nichtleere Teilmenge
![]() heißt Teilraum
(oder Unterraum) von
heißt Teilraum
(oder Unterraum) von ![]() , falls gilt:
, falls gilt:
![]() ein
ein ![]() -Vektorraum,
-Vektorraum, ![]() ,
, ![]() . Dann heißt die
Menge
. Dann heißt die
Menge
![]() ein
ein ![]() -Vektorraum und
-Vektorraum und
![]() . Die Menge
. Die Menge
![]() ein
ein ![]() -Vektorraum. Eine Menge
-Vektorraum. Eine Menge
![]() heißt Erzeugendensystem
von
heißt Erzeugendensystem
von ![]() , falls
, falls
![]() . Eine Familie in V
heißt Basis falls sie ein linear unabhängiges
Erzeugendensystem bildet. Ein Vektorraum heißt endlich erzeugt,
falls er ein endliches Erzeugendensystem besitzt.
. Eine Familie in V
heißt Basis falls sie ein linear unabhängiges
Erzeugendensystem bildet. Ein Vektorraum heißt endlich erzeugt,
falls er ein endliches Erzeugendensystem besitzt.
![]() ein
ein ![]() -Vektorraum und sei
-Vektorraum und sei
![]() eine Familie von Vektoren aus
eine Familie von Vektoren aus ![]() . Folgende Aussagen sind äquivalent:
. Folgende Aussagen sind äquivalent:
![]() ein
ein ![]() -Vektorraum
der endlich erzeugt ist. Sei
-Vektorraum
der endlich erzeugt ist. Sei
![]() eine
Basis von
eine
Basis von ![]() und sei
und sei
![]() für
für
![]() . Dann folgt aus
. Dann folgt aus
![]() ist eine Basis von
ist eine Basis von ![]() .
.
![]() eine Basis der endlich erzeugten Vektroraumes
eine Basis der endlich erzeugten Vektroraumes ![]() , und sei
, und sei
![]() eine linear unabhängige Familie in
eine linear unabhängige Familie in ![]() . Dann gilt
. Dann gilt ![]() , und
es existieren Indizes
, und
es existieren Indizes
![]() ,
so dass
,
so dass
![]() eine Basis von
eine Basis von ![]() sind.
sind.
![]() ein
ein ![]() Vektoraum, so heißt
Vektoraum, so heißt