Definition

Next: Matrizen Up: Quadratische Formen Previous: Quadratische Formen Contents Index

Subsections

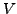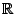Sei ein $\mathbb{R}$ -Vektorraum

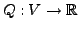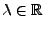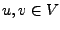Eine Abbildung $Q:V\rightarrow\mathbb{R}$ heißt quadratische Form, falls für alle $\lambda\in\mathbb{R}$ , $u,v\in V$ gilt

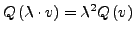
$Q\left(\lambda\cdot v\right)=\lambda^{2}Q\left(v\right)$
Folgendes ist eine symmetrische Bilinearform

$\displaystyle \beta_{Q}$ $\displaystyle :$ $\displaystyle V\times V\rightarrow\mathbb{R}$

$\displaystyle :$ $\displaystyle \left(u,v\right)\mapsto\frac{1}{2}\left(Q\left(u+v\right)-Q\left(u\right)-Q\left(v\right)\right)$

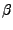Sei $\beta$ eine beliebige symmetrische Bilinearform auf 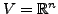$V=\mathbb{R}^{n}$ . Dann ist

$\displaystyle Q:V\rightarrow\mathbb{R}:v\mapsto\beta\left(v,v\right)$

eine quadratische Form.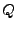

heißt die zu 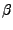$\beta$ assoziierte quadratische Form.

Die Beziehungen aus diesem und dem letzten Punkt zwischen quadratischer Form und Bilinearform gelten allgemein über beliebigen Körpern, in denen 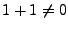$1+1\neq0$ gilt.

Marco Möller 20:09:10 02.12.2005

$\displaystyle \beta_{Q}$	$\displaystyle :$	$\displaystyle V\times V\rightarrow\mathbb{R}$
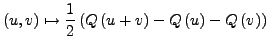
	$\displaystyle :$	$\displaystyle \left(u,v\right)\mapsto\frac{1}{2}\left(Q\left(u+v\right)-Q\left(u\right)-Q\left(v\right)\right)$