




Next: Interferenz
Up: Wellenausbreitung in mehreren Dimensionen
Previous: Wellenausbreitung in mehreren Dimensionen
Contents
Index
- Wellenvektor
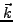 mit
mit
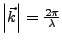 und in Richtung der Ausbreitungsrichtung der Wellenfronten
und in Richtung der Ausbreitungsrichtung der Wellenfronten
- Harmonische eben Welle
-
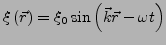
- Kugelwelle
-
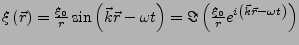
- Energiedichte
- das Integral über der Energiedichte
muss auf einer geschlossenen Oberfläche konstant sein. Da die Amplitude
quadratisch in die Energiedichte eingeht, muss bei der Kugel mit
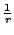 multipliziert werden, und nicht mit
multipliziert werden, und nicht mit
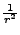
Marco Möller 16:43:44 24.10.2005