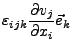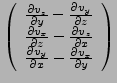Next: Krummlinige Koordinatensysteme
Up: Vektoren und Felder im
Previous: Vektoren im Raum
Contents
Index
Subsections
Elemente der Vektoranalysis
- wenn nach der Zeit (
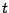 ) Abgeleitet wird, kann man dies auch so abkürzen:
) Abgeleitet wird, kann man dies auch so abkürzen:
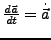
- Produktregel
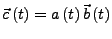
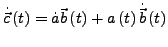
Vektorielle differentiation eines Skalarfeldes
Totales Differential:
- Errechnen einer Ableitung eines Vektorfeldes:
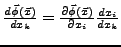
-
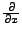 ist die partielle Ableitung
nach
ist die partielle Ableitung
nach 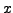 , wobei alle anderen Variablen als Konstanten betrachtet
werden.
, wobei alle anderen Variablen als Konstanten betrachtet
werden.
- Satz von Schwarz
Wenn die gemischten partiellen Ableitungen (bis zur zweiten) von einer
Funktion stetig sind in einem Bereich 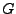 . Dann gilt das die Reihenfolge
der Ableitungen im Innern vertauscht werden kann. Wenn dieses gilt,
existiert das totale Differential.
. Dann gilt das die Reihenfolge
der Ableitungen im Innern vertauscht werden kann. Wenn dieses gilt,
existiert das totale Differential.
- Flächen für die
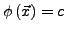 sind werden Äquipotentialflächen
bezeichnet.
sind werden Äquipotentialflächen
bezeichnet.
Das Nabla-Symbol
- Hiermit lässt sich das totale differential auch als Skalarprodukt
schreiben, indem man die zu differenzierende Funktion vorher mit
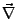 und anschließenden mit
und anschließenden mit 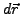 Multipliziert.
Multipliziert.
-
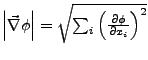
Der Gradient von 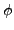 lässt sich wie folgt
berechnen
lässt sich wie folgt
berechnen
Die Richtungsableitung gibt die
Steigung an, die man im Punkt 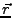 enthält, wenn man ich Richtung
des Einheitsvektors
enthält, wenn man ich Richtung
des Einheitsvektors 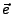 laufen würde.
laufen würde.
Der Laplaceoperator ist ein skalaerer
Differentialoperator (er ordnet einem Vektor einen Vektor, und einem
Skalar einen Skalar zu). Er ist wie folgt definiert:
 ist invariant (verändet sich nicht) unter Koordinatenspigelung
(= Paritätsinvariant)
ist invariant (verändet sich nicht) unter Koordinatenspigelung
(= Paritätsinvariant)
-
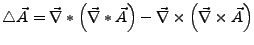
-
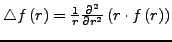
Divergenz
Die Divergenz eines Vektorfeldes
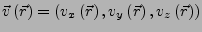 ist wie folgt definiert (
ist wie folgt definiert ( = Skalarprodukt):
= Skalarprodukt):
- Auf Reihenfolge der Schreibweise achten.
- Felder mit
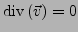 nennen sich:
nennen sich:
- Divergenzfrei
- Quellenfrei
- Konvervative Kraftfelder (mit Energieerhaltung
/ Unabhängigkeit des Weges)
Rotation
Die Rotation eines Vektorfeldes
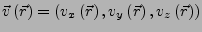 ist wie folgt definiert:
ist wie folgt definiert:
- Auf Reihenfolge der Schreibweise achten.
- Felder mit
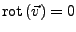 nennen sich:
nennen sich:
- Rotationsfrei
- Wirbelfrei
- konservative Felder





Next: Krummlinige Koordinatensysteme
Up: Vektoren und Felder im
Previous: Vektoren im Raum
Contents
Index
Marco Möller 20:36:18 26.01.2006
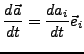
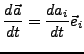
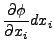
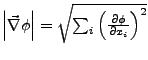
![]() lässt sich wie folgt
berechnen
lässt sich wie folgt
berechnen
![]() enthält, wenn man ich Richtung
des Einheitsvektors
enthält, wenn man ich Richtung
des Einheitsvektors ![]() laufen würde.
laufen würde.
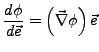
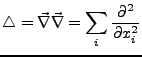
![]() ist wie folgt definiert (
ist wie folgt definiert (![]() = Skalarprodukt):
= Skalarprodukt):
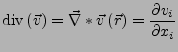
![]() ist wie folgt definiert:
ist wie folgt definiert: