Jeder Punkt im
![]() ist durch Angabe von
ist durch Angabe von ![]() Zahlen
Zahlen
![]() festgelegt. Insbesondere durch die karthesischen
Koordinaten
festgelegt. Insbesondere durch die karthesischen
Koordinaten ![]() . Es gibt also
eine eineindeutige (bijektive) Zuordnung.
. Es gibt also
eine eineindeutige (bijektive) Zuordnung.
Der Ortsvektor hat nun folgende Gestalt:
Unter Koordinatenlinien versteht
man Linien, durch den Raum, bei denen jeweis alle Variablen bis auf
![]() bestgehalten werden. Bei krummlinigen Koordinaten
ist mindestens eine solche Linie keine Gerade. Diese schneiden sich
im Punkt
bestgehalten werden. Bei krummlinigen Koordinaten
ist mindestens eine solche Linie keine Gerade. Diese schneiden sich
im Punkt
![]() :
:
Genauso lassen sich Koordinatenflächene
definieren. Auch diese schneiden sich im Punkt
![]() :
:
Für das neue Koordinatensystem lassen sich Einheitsvektoren errechen.
Diese sind aber im Allgemeinen nicht im Raum konstant, sondern verändern
sich je nach Lage im Raum. Sie werden daher als mitgeführtes
Dreibein bezeichnen. Sie lassen sich
wie folgt berechnen:
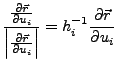 |
|||
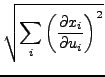 |
![]() wird als Maßfaktor
bezeichnet.
wird als Maßfaktor
bezeichnet.
Hier werden die Punkte im Raum über die ![]() Variablen
Variablen
![]() .
.
![]() ist dabei der Winkel zwischen der positiven
ist dabei der Winkel zwischen der positiven ![]() -Achse
und der Projektion von
-Achse
und der Projektion von ![]() auf die
auf die ![]() Ebene und
Ebene und ![]() die Länge vom dieses Projezierten Vektors.
die Länge vom dieses Projezierten Vektors. ![]() ist identisch mit
dem
ist identisch mit
dem ![]() aus den Karthesischen Koordinaten.
aus den Karthesischen Koordinaten.
![]() sind Geraden
und
sind Geraden
und ![]() ist ein Kreis.
ist ein Kreis. ![]() ist ein Kreiszylinder und
ist ein Kreiszylinder und
![]() sind Ebenen. Diese Variablen sind in Ihrem Wertebereich
auf
sind Ebenen. Diese Variablen sind in Ihrem Wertebereich
auf
![]() ,
,
![]() und
und
![]() beschränkt. Der Ursprung (
beschränkt. Der Ursprung (![]() ) ist in diesen Koordinaten nicht
eindeutig bestimmt.
) ist in diesen Koordinaten nicht
eindeutig bestimmt.
| 0 |
Hier werden die Punkte im Raum über die ![]() Variablen
Variablen
![]() .
.
![]() ist dabei der Winkel zwischen der positiven
ist dabei der Winkel zwischen der positiven ![]() -Achse
und der Projektion von
-Achse
und der Projektion von ![]() auf die
auf die ![]() Ebene.
Ebene. ![]() ist der Winkel zwischen
ist der Winkel zwischen ![]() und der positiven
und der positiven ![]() -Achse.
-Achse. ![]() ist die Länge des Vektros
ist die Länge des Vektros ![]() .
. ![]() ist eine Gerade und
ist eine Gerade und
![]() sind (halb) Kreise.
sind (halb) Kreise. ![]() ist ein Kugeloberfläche,
ist ein Kugeloberfläche,
![]() ist eine Halbebenen und
ist eine Halbebenen und ![]() ein Trichter. Diese Variablen
sind in Ihrem Wertebereich auf
ein Trichter. Diese Variablen
sind in Ihrem Wertebereich auf
![]() ,
,
![]() und
und
![]() beschränkt. Die gesamte
beschränkt. Die gesamte
![]() -Achse ist in Ihren Koordinaten nicht eindeutig bestimmst.
-Achse ist in Ihren Koordinaten nicht eindeutig bestimmst.
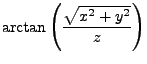 |
|||
 |
|||
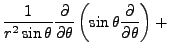 |
|||
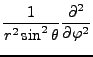 |
Diese Koordinaten haben den Vorteil, das die Koordinaten linien für
![]() und
und ![]() Parabeln beschreiben, deren Brennpunkt im Ursprung
des Systems liegt. Die Koordinatenlinen für
Parabeln beschreiben, deren Brennpunkt im Ursprung
des Systems liegt. Die Koordinatenlinen für ![]() sind Kreise.
sind Kreise.
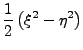 |
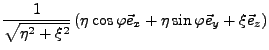 |
|||
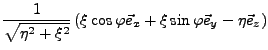 |
|||
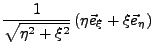 |
|||
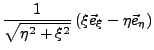 |
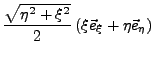 |