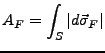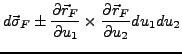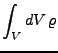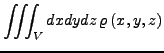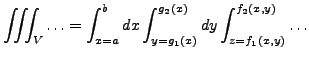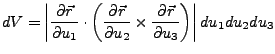Next: Differentialgleichungen
Up: Vektoren und Felder im
Previous: Differentiation in krummlinigen Koordinatensystemen
Contents
Index
Subsections
Parameterisierung der Bahnkurve
Menge aller Punkte zwischen
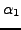 und
und
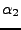 gibt die
Bahnkurve
gibt die
Bahnkurve
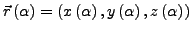 .
Hierbei ist
.
Hierbei ist 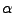 der Bahnparameter
der die Bahnkurve parameterisiert.
der Bahnparameter
der die Bahnkurve parameterisiert.
Spezielle Bahnparameter sind 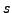 die Bogenlänge,
und
die Bogenlänge,
und 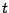 die Zeit.
die Zeit.
- Der Wert des Integrals hängt nich von der Parameterisierung ab, solange
sie den gleichen Weg beschreiben
Weglänge einer Bahnkurve
Sei
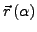 eine Parameterisierung des zu messenden
Weges. Die Weglänge ergibt sich dann für
eine Parameterisierung des zu messenden
Weges. Die Weglänge ergibt sich dann für
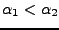
Flächenintegrale
Hierzu benötigt man eine Funktion
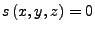 die eine
Fläche beschreibt. Wenn sich diese nach
die eine
Fläche beschreibt. Wenn sich diese nach
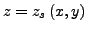 umstellen lässt
umstellen lässt 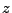 , kann man das Flächenintegral über der Funktion
, kann man das Flächenintegral über der Funktion
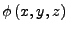 wie folgt schreiben
wie folgt schreiben
Vektorelle Flächenintegrale
Hierzu benötigt man eine Konvention, die der orientierten Flächen:
Der Vektor
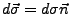 steht senkrecht auf der
Oberfläche und zeigt immer nach Außen. Je nachem ob wo mam sich auf
der Koordinatenachse befindet gilt:
steht senkrecht auf der
Oberfläche und zeigt immer nach Außen. Je nachem ob wo mam sich auf
der Koordinatenachse befindet gilt:
Sei
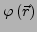 ein Skalar- und
ein Skalar- und
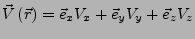 ein Vektorfeld. Es lassen sich nun folgende Integrale definieren:
ein Vektorfeld. Es lassen sich nun folgende Integrale definieren:
- Es gilt
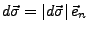 . Falls
eine Komponente von
. Falls
eine Komponente von
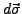 und auch
und auch
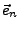 bekannt
ist lässt sichhieraus der Betrag und damit das geamte
bekannt
ist lässt sichhieraus der Betrag und damit das geamte
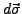 rekonstruieren. Z.B.
rekonstruieren. Z.B.
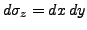 und
und
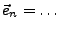 .
.
Oberflächenberechnung
Die Oberläche 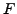 einer Funktion
einer Funktion 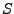 lässt sich mit Hilfe von vektoriellen
Flächenintegralen sehr leicht bestimmen. Hierzu muss ein
lässt sich mit Hilfe von vektoriellen
Flächenintegralen sehr leicht bestimmen. Hierzu muss ein
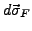 gefunden werden, welches auf der gesamten Fläche rechtwiklig steht
und dessen länge der größe der Flächenelemente entspricht. Dieses
gefunden werden, welches auf der gesamten Fläche rechtwiklig steht
und dessen länge der größe der Flächenelemente entspricht. Dieses
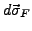 lässt sich auf verschiedene Arten gewinnen. Entweder
man nutzt ein bereits bekanntes Koordinatensystem, falls die gewünschte
Fläche dort einer Koordinatenfläche (bzw. einem Teil davon) entspricht.
Oder man definiert sich entsprechend ein neues. Die Fläche ist hiermit
nun
lässt sich auf verschiedene Arten gewinnen. Entweder
man nutzt ein bereits bekanntes Koordinatensystem, falls die gewünschte
Fläche dort einer Koordinatenfläche (bzw. einem Teil davon) entspricht.
Oder man definiert sich entsprechend ein neues. Die Fläche ist hiermit
nun
- Es lässt sich auch ein neues
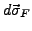 wie folgt definieren.
Die Fläche
wie folgt definieren.
Die Fläche 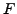 lasse sich in der Form
mit
lasse sich in der Form
mit 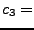 konstant schreiben. Dann gilt:
Wobei das Vorzeichen so gewählt werden muss, das es auf geschlossenen
Flächen nach außen zeigt.
konstant schreiben. Dann gilt:
Wobei das Vorzeichen so gewählt werden muss, das es auf geschlossenen
Flächen nach außen zeigt.
Volumenintegrale
Hierbei wird ein Dreifachintegral über alle drei Raumkoordinaten bestimmt.
Die Grenzen können dabei im allgemeinen voneinander abhängen.
- Die abhängigen Grenzen können z.B. so behandelt werden:
- Für belibige Koordinatensysteme gilt außer den vorher genannten Beziehungen:
Integralsätze
- All diese Sätze gelten nur, wenn es auf beiden Seiten möglich ist,
divergenten Punkten auszuweichen. Wenn z.B. eine Fläche immer durch
einen Punkt läuft, der divergiert egal wie man sie legt, dann gelten
all diese Sätze nicht.
- Die Keise um die Integrale bedeuten, dass über geschlossene Flächen
/ Linien integriert werden muss.
- Bei Kruvenumläufen wird gegen den Uhrzeigersinn positiv gezählt. Es
gilt (Orientierung der Zirkulatuion):
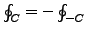
- Gauß'scher Satz
-
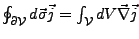
- Integral der Quelldichte ist gleich dem Fluss durch die Randflächen
- Kontinuitätsgleichung
-
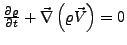
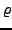 ist die Dichte des Mediums
ist die Dichte des Mediums
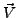 ist die Strömungsgeschdingkeit
ist die Strömungsgeschdingkeit
- Gilt nur für quellenfreie Felder. Bedeutet, dass die Summe aus Abnahme
von z.B. Masse in einer Region und der Fluss durch dessen Begrenzung
0 ergibt.
- Green'scher Integralsatz
-
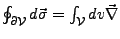
- Dies sind Differentialoperatoren. Sie wirken auf die hinter ihnen
stehende Gleichung genau gleich
- z.B.
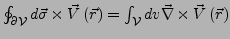
- Green'scher Satz
-
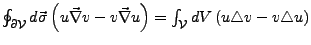
- Satz von Stokes
-
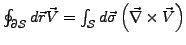
- Potentialfeld
-
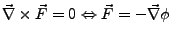
- auch konservatives Feld genannt.
- Oberfläche
-
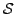 ist Symbol für geschlossene
Fläche
ist Symbol für geschlossene
Fläche
- Volumen
-
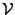 ist Symbol für zusammenhängendes
Volumen
ist Symbol für zusammenhängendes
Volumen
- Begrenzung
-
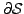
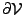 Begrenzungskurve / Fläche einer Oberfläche / Volumen
Begrenzungskurve / Fläche einer Oberfläche / Volumen





Next: Differentialgleichungen
Up: Vektoren und Felder im
Previous: Differentiation in krummlinigen Koordinatensystemen
Contents
Index
Marco Möller 20:36:18 26.01.2006
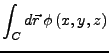
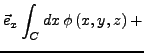
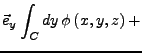
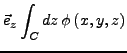
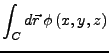
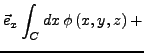
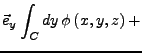
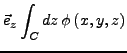
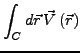
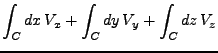
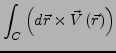
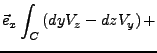
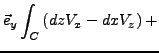
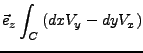
![]() und
und
![]() gibt die
Bahnkurve
gibt die
Bahnkurve
![]() .
Hierbei ist
.
Hierbei ist ![]() der Bahnparameter
der die Bahnkurve parameterisiert.
der Bahnparameter
der die Bahnkurve parameterisiert.
![]() die Bogenlänge,
und
die Bogenlänge,
und ![]() die Zeit.
die Zeit.
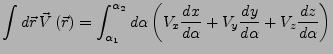
![]() eine Parameterisierung des zu messenden
Weges. Die Weglänge ergibt sich dann für
eine Parameterisierung des zu messenden
Weges. Die Weglänge ergibt sich dann für
![]()
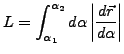
![]() die eine
Fläche beschreibt. Wenn sich diese nach
die eine
Fläche beschreibt. Wenn sich diese nach
![]() umstellen lässt
umstellen lässt ![]() , kann man das Flächenintegral über der Funktion
, kann man das Flächenintegral über der Funktion
![]() wie folgt schreiben
wie folgt schreiben
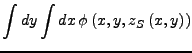
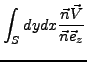
![]() steht senkrecht auf der
Oberfläche und zeigt immer nach Außen. Je nachem ob wo mam sich auf
der Koordinatenachse befindet gilt:
steht senkrecht auf der
Oberfläche und zeigt immer nach Außen. Je nachem ob wo mam sich auf
der Koordinatenachse befindet gilt:
![]() ein Skalar- und
ein Skalar- und
![]() ein Vektorfeld. Es lassen sich nun folgende Integrale definieren:
ein Vektorfeld. Es lassen sich nun folgende Integrale definieren:
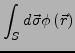
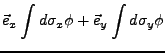
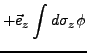
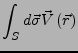
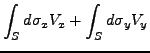
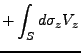
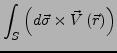
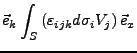
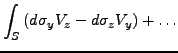
![]() einer Funktion
einer Funktion ![]() lässt sich mit Hilfe von vektoriellen
Flächenintegralen sehr leicht bestimmen. Hierzu muss ein
lässt sich mit Hilfe von vektoriellen
Flächenintegralen sehr leicht bestimmen. Hierzu muss ein
![]() gefunden werden, welches auf der gesamten Fläche rechtwiklig steht
und dessen länge der größe der Flächenelemente entspricht. Dieses
gefunden werden, welches auf der gesamten Fläche rechtwiklig steht
und dessen länge der größe der Flächenelemente entspricht. Dieses
![]() lässt sich auf verschiedene Arten gewinnen. Entweder
man nutzt ein bereits bekanntes Koordinatensystem, falls die gewünschte
Fläche dort einer Koordinatenfläche (bzw. einem Teil davon) entspricht.
Oder man definiert sich entsprechend ein neues. Die Fläche ist hiermit
nun
lässt sich auf verschiedene Arten gewinnen. Entweder
man nutzt ein bereits bekanntes Koordinatensystem, falls die gewünschte
Fläche dort einer Koordinatenfläche (bzw. einem Teil davon) entspricht.
Oder man definiert sich entsprechend ein neues. Die Fläche ist hiermit
nun