Next: Elektrostatik
Up: Hamiltonsche Formulierung der Mechanik
Previous: Variationsproblem
Contents
Index
Subsections
Das Hamiltonische Prinzip
- Prinzip der kleinsten Wirkung
- Wirkungsintegral
-
- Eichfreiheit
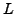 nur bestimmt bis auf eine totale Zeitableitung einer Funktion
nur bestimmt bis auf eine totale Zeitableitung einer Funktion
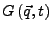 .
.
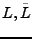 führen auf die gleichen Bewegungsgleichungen.
führen auf die gleichen Bewegungsgleichungen.
- Vorteile
- des Hamiltonischen Prinzips
- es ist kompakt + elegant
- es ist immer von gleicher Form, unabhängig von der Wahl eines Koordinatensystems
- läßt sich relativistisch verallgemeinern, anwendbar in Quantenmechanik
- anwendbar in Kontinuumsmechanik, Elektrodynamik (funktioniert auch
für Felder!)
- Verallgemeinerte Koordinaten
- werden Transformiert von
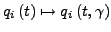 mit
mit
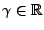 .
.
- Wir erhalten also eine Geradenschaar
-
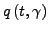 muss so beschaffen sein, das die Lagrangegleichung
für alle
muss so beschaffen sein, das die Lagrangegleichung
für alle
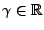 erfüllt ist
erfüllt ist
- Invariant
- unter der Transformation von
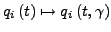 ist
ist
- auch Noether Theorem genannt
- Hierraus folgt aus:
- Translationsinvarianz
- freie Ursprungswahl
im Raum die Impulserhaltung
- Rotationsinvarianz
- isotropie
des Raumes (Richtungsunabhängigkeit) die Drehimpulserhaltung
- Zeitverschiebung
- Energieerhaltung
- Gallileiinvarianz
- Schwerpunktsimpulserhaltung
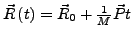
| # |
Erhaltungsgröße |
Transformation |
| 3 |
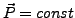 |
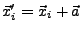 |
| 3 |
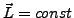 |
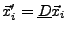 |
| 1 |
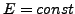 |
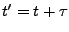 |
| 3 |
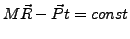 |
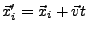 |
- allgemeines Noether Theorem
-
- siehe des:Eichfreiheit (Eichfreiheit).
- Invariant ist damit
-
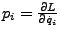 verallgemeinerter
Impuls
verallgemeinerter
Impuls
-
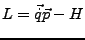
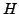 ist die negative Legendre Transformierte von
ist die negative Legendre Transformierte von 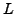
Legendre Transformation
- gegeben
-
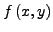
- gesucht
-
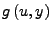 mit
mit
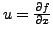 wobei
wobei 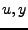 unabhängig sind
unabhängig sind
- Rücktransformation
-
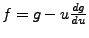
Hamiltonische Bewegungsgleichungen
- die ersten beiden Gleichungen ergeben
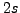 DGL. 1.Ordnung. Dies sind
doppelt so viele wie bei Lagrange 2, allerdings dafür nur von der
``halben'' Ordnung. Dies ist numerisch günstiger
DGL. 1.Ordnung. Dies sind
doppelt so viele wie bei Lagrange 2, allerdings dafür nur von der
``halben'' Ordnung. Dies ist numerisch günstiger
-
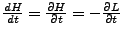
- Phasenraum
-
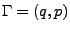
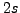 Dimensional
Dimensional
- Energie
-
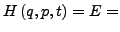 Gesamtenergie
Gesamtenergie
- Falls
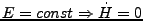 ist die Lösung eine
ist die Lösung eine 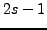 dimensionale
Hyperfläche in
dimensionale
Hyperfläche in 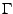
Man definiert für ein physikalisches System mit 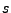 verallgemeinerten
Koordinaten
verallgemeinerten
Koordinaten 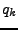 und
und 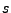 verallgemeinerten Impulsen
verallgemeinerten Impulsen 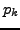 ,
,
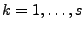 , für zwei Funktionen
, für zwei Funktionen
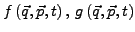 die Poisson-Klammer
die Poisson-Klammer
-
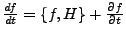
-
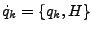 und
und
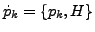
-
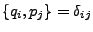
-
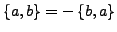
-
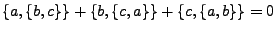
- Gilt
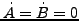 , dann auch
, dann auch
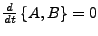
- Gilt
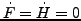 , dann auch
, dann auch
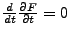





Next: Elektrostatik
Up: Hamiltonsche Formulierung der Mechanik
Previous: Variationsproblem
Contents
Index
Marco Möller 12:12:15 01.03.2006
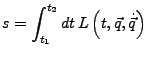
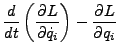
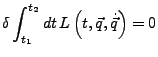
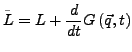
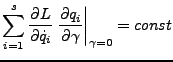
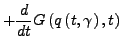
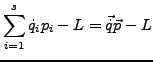
![]() verallgemeinerten
Koordinaten
verallgemeinerten
Koordinaten ![]() und
und ![]() verallgemeinerten Impulsen
verallgemeinerten Impulsen ![]() ,
,
![]() , für zwei Funktionen
, für zwei Funktionen
![]() die Poisson-Klammer
die Poisson-Klammer