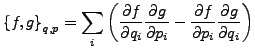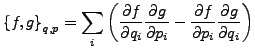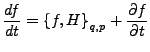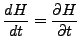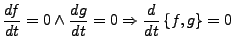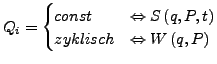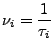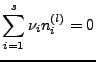Next: Elektrodynamik
Up: Hamilton Jakobi Theorie
Previous: Hamiltonische charakteristische Funktion
Contents
Index
Subsections
Wirkungs- und Winkelvariable
Poisson-Klammern
- Zweck
- Konstanten der Bewegung und Bewegungsgleichungen kompakt
darstellen (formaler Übergang zur QM einfach)
- Observable
- ist
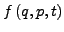 mit
mit
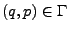 (Phasenraumpunkt)
(Phasenraumpunkt)
- zeitliche Änderung
-
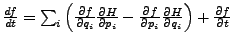
- Poisson-Klammern
- für
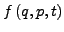 und
und
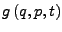
- nach den angegebenen Indizes differenzieren
-
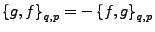
-
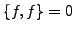
-
-
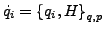 english
english
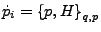
- fundamentale
- Poisson-Klamern
-
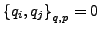
-
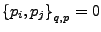
-
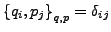
- wenn diese Eigenschaften gelten sind die
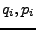 ein satz unabhängiger
Variablen
ein satz unabhängiger
Variablen
- Koordinatenunabhängigkeit
- falls
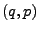 und
und
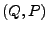 beide genügen der Hamiltonischen Bewegungsgleichung,
beide genügen der Hamiltonischen Bewegungsgleichung,
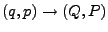 kanonisch
kanonisch
dann gilt
- Weiter ist
- der Wert der poissonklammer unabhängig von der Wahl
der Koordinaten im Phasenraum.
- d.h. wir können die Koordinatenindizies weglassen!
- Formale Eigenschaften
- der Poissson-Klammern (
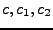 sind Konstanten)
sind Konstanten)
- Antisymmetrie
-
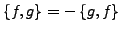
- Bi-Linearität
-
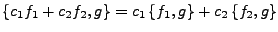
- Nullelement
-
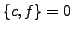
- Produktregel
-
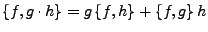
- Jakobi-Identität
-
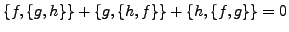
- Integral der Bewegung
- ist ein
anderer Begriff für Erhaltungsgrößen. Eine Größe die entlang der Bahnkurve
eines freien Teilchens erhalten ist.
- Observable
-
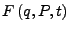 sei eine mech. Observable
sei eine mech. Observable
- Poissonscher Satz
- Die Poisson-Klammer
zweier Integrale der Bewegung ist wieder ein Integral der Beweung.
Periodizität
- periodisch
-
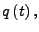
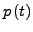
- Libration
- falls
- Rotation
- falls
- starrer Rotor
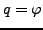
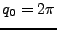
- Es können in physikalischen Systemen beide Arten auftreten
- System
- ein System in
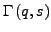 mit
mit 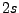 Dimesionen
ist periodisch, falls Projektion auf jede Ebene
Dimesionen
ist periodisch, falls Projektion auf jede Ebene
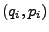 periodisch ist. Die einzelnen Perioden seien
periodisch ist. Die einzelnen Perioden seien 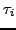 . Falls
. Falls
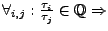 geschlossene Bahn im
geschlossene Bahn im 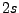 -dim. Phasenraum, andernfalls bedingt
periodisch.
-dim. Phasenraum, andernfalls bedingt
periodisch.
- Ziel
- Periodenfrequenzen des Systems bestimmen
- Vorgehen
- Zuerst normal Lösen über
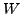 danach
danach 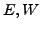 mit
mit 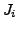 ausdrücken und Ableiten
ausdrücken und Ableiten
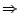 Frequenzen
Frequenzen
- Spezialfall
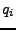 zyklisch
zyklisch
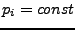
- Entartung
- Bewegung im
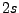 -dim
-dim 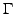 periodisch,
falls jede der
periodisch,
falls jede der 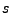 -Projektionen auf eine
-Projektionen auf eine
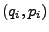 -Ebene
periodisch ist. Die Frequenz
ist im Prinzip für alle
-Ebene
periodisch ist. Die Frequenz
ist im Prinzip für alle 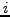 verschieden.
verschieden.
- Phasenbahn
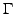 ist abgeschlossen (einfach Periodisch) falls
ist abgeschlossen (einfach Periodisch) falls
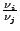 rational ist für alle
rational ist für alle 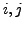
- bedingt periodisch
- wird sie im anderen
Fall genannt.
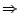 Phasenbahn nicht geschlossen
Phasenbahn nicht geschlossen
- Frequenzverhältnis
- läss sich im abgeschlossenen Fall angeben
-
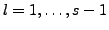
-
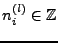
- jeweils nicht alle
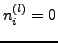 für ein
für ein 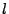
- o.B.d.A. (umsortieren der Unabhängigen nach hinten)
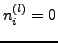 für
für
![$ i\in\left[m+1,s\right]$](img416.png)
- die Vektoren
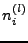 müssen zueinander linear unabhängig
sein
müssen zueinander linear unabhängig
sein
- m-Fache
- Entartung haben wir, falls es nur
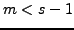 solcher Zahlensätze
solcher Zahlensätze
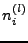 gibt
gibt





Next: Elektrodynamik
Up: Hamilton Jakobi Theorie
Previous: Hamiltonische charakteristische Funktion
Contents
Index
Marco Möller 20:49:26 12.02.2007