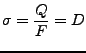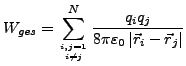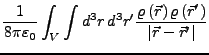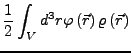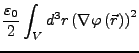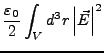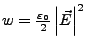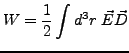Next: Magnetostatik in Materie
Up: Elektrodynamik
Previous: Elektrodynamik
Contents
Index
Subsections
Elektrodynamik der Dielektrika
- Ziel
-
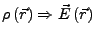
- Anforderungen
- an Materie
- Gesamtladung der Materie
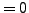
- es fließt kein Strom
- anders als bei Metallen
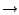
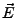 -Feld
-Feld 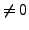 innerhalb
innerhalb
- Materie ist ``polarisierbar''
- Polarisationsladungsdichte
-
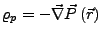
- Gesamtladungsdichte
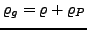
-
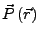 lokales Dipolmoment / Polarisation
lokales Dipolmoment / Polarisation
-
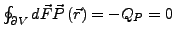
- Flächenladungsdichte
-
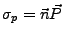
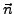 Normalenvektor auf dem Volumen
Normalenvektor auf dem Volumen
- Dielektrische Verschiebung
-
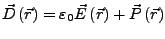
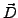 wird von den überschussladungen
wird von den überschussladungen 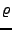 erzeugt und
ist damit unabhängig vom Material, während
erzeugt und
ist damit unabhängig vom Material, während
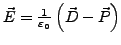 über
über 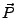 vom Material abhängt.
vom Material abhängt.
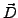 ist nur Hilfsgröße,
ist nur Hilfsgröße, 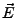 ist die eigentliche physikalische
Größe
ist die eigentliche physikalische
Größe
- Maxwell Gleichung
- der Elektrostatik mit Dielektrikum
- Deformationspolarisation
- es
gibt keine elementaren Dipole im Material ohne äußeres Feld. Das Dipolmoment
wird beim Anlegen des äußeren Feldes durch Verschieben der im Atom
oder Molekühl gebundenen Ladungen erzeugt (Deformation der Ladungsverteilung).
- Paraelektrika
- Es gibt molekulare Dipole
(``Elementardipole'') wie zB. Wasser.
Diese richten sich durch das externe Feld bis zu einem gewissen Grad
aus. Die braunsche Molekularbewegung wirkt gegen die Orientierung.
D.h. die Polarisierung ist temperaturabhängig. Ohne Externes Feld
ist die Polarisation 0
- Ferroelektrika
- Stoffe mit molekularen
Dipolen, die sich unterhalb einer kritischen Temperatur
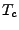 (Curie-Temperatur)
spontan, d.h. ohne äußeres Feld ausrichten.
(Curie-Temperatur)
spontan, d.h. ohne äußeres Feld ausrichten.
- Im Allgemeinen sind die äußeren Felder klein gegen die molekularen
bzw. atomaren Felder.
- linear Response
- für nicht zu starke Felder
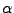 ist eine Matrix für anisotropes Dielektrikum
ist eine Matrix für anisotropes Dielektrikum
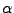 ist ein Skalar für isotropes Dielektrikum
ist ein Skalar für isotropes Dielektrikum
- elektrische Suszeptibilität
-
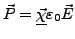
- Dielektrizitätstensor
-
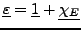
- isotrope Dielektrika gibt es auchenglish
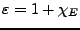
- Konvention im Folgenden
- Es wird soweit nicht anders angegeben
von einem isotropen linearen Medium ausgeganden.
Plattenkondensator
- Kapazität
-
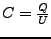
- Plattenkondensator
-
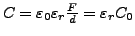
- Kondensatoroberfläche
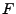
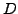 betrag der dielektrischen Verschiebung
betrag der dielektrischen Verschiebung
- Maxwellgleichungen haben selbe Struktur
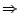 selbe Lösungsansätze
(Poisson-Gl.)
selbe Lösungsansätze
(Poisson-Gl.)
- Grenzschichten
- haben folgendes Stetigkeitsverhalten
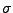 Ladungsdichte auf der Grenzschicht
Ladungsdichte auf der Grenzschicht
- Stetigkeit in Komponenten
- bei ungeladene Grenzschicht
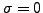 zusätzlich:
zusätzlich:
- Durch Einbringen von Spiegelladungen lassen sich Felddeformationen
durch Grenzschichten berücksichtigen. Deren Ort ist gespiegel, allerdings
haben sie einen zur Stetigkeitsbedingung passenden Wert.
Elektrostatische Energie
- Punktladungen im Vakuum
- an den Orten
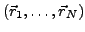 mit Ladungen
mit Ladungen
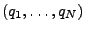
- Kontinuierliche
- Ladungsverteilung
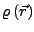
- Energiedichte
-
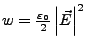
-
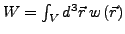
- Beim Überprüfen mit einer diskreten Verteilung gibt es
- Sebstenergiedichte
- diese ist divergent
für homogen geladene Kugel mit
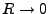 . Problem für Elektron.
Gelöst in Qantenfeldtheorie
. Problem für Elektron.
Gelöst in Qantenfeldtheorie
- Wechselwirkungsanteil
- entspricht
der Diskreten energieformel
- Feldenergie im Dielektrikum
-





Next: Magnetostatik in Materie
Up: Elektrodynamik
Previous: Elektrodynamik
Contents
Index
Marco Möller 20:49:26 12.02.2007